hihocoder #1529 : 不上升序列

Description

给定一个长度为 n 的非负整数序列 a[1..n]。
你每次可以花费 1 的代价给某个 a[i] 加1或者减1。
求最少需要多少代价能将这个序列变成一个不上升序列。

Solution

容易想到一个 (dp),设 (f[x][i]) 表示前 (x) 个数,最小的数不小于 (i) 的最小代价
(f[x][i]=f[x-1][i]+|a_x-i|)
其实这是两条折线合并的过程,(|a_x-i|) 是一条以 (a_x) 为拐点的折线,且两条直线的斜率分别为 (1,-1)
对于 (f[x][i]) 也是一条折线或直线,显然在拐点处的解是最优的(也就是斜率变成 (0) 的位置,折线是不会穿过 (x) 轴的,所以肯定存在斜率为 (0) 的位置)

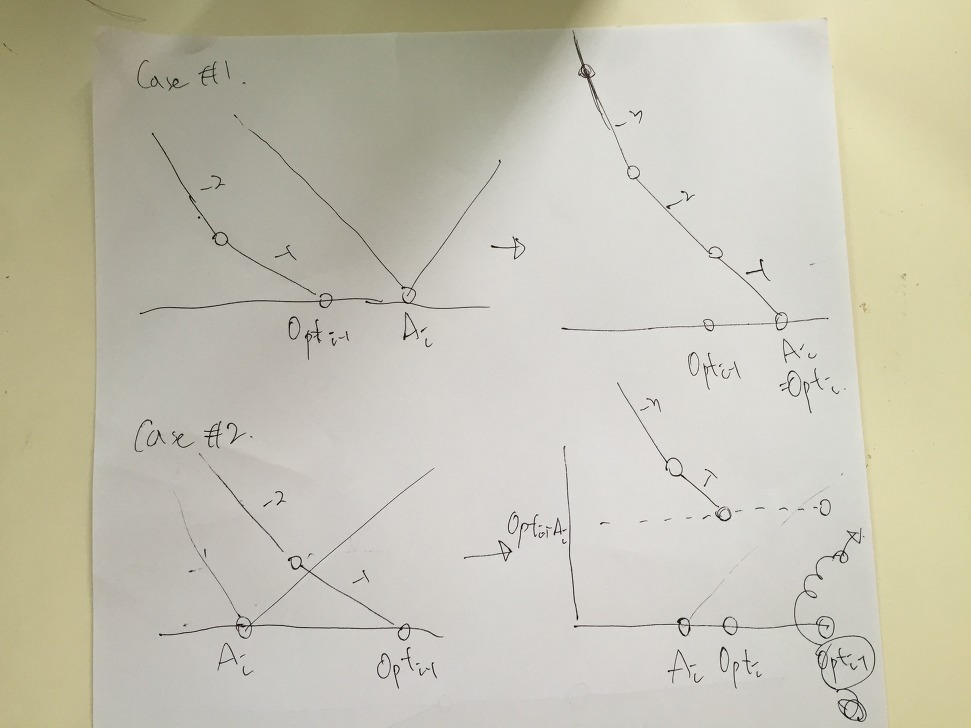
我们分两种情况合并这两条折线

观察图片发现:新图也就是把原图中的两条折线的每一段的斜率分别相加

这里的拐点也就是使得斜率发生改变的地方,因为斜率发现改变的地方都有可能成为斜率为 (0) 的那个拐点
用堆维护拐点的横坐标就可以了

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
priority_queue<int>Q;
int main()
{
	freopen("pp.in","r",stdin);
	freopen("pp.out","w",stdout);
	int n,x;long long ans=0;
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		x=-x;Q.push(x);
		if(Q.top()>x)ans+=Q.top()-x,Q.pop(),Q.push(x);
	}
	printf("%lld
",ans);
	return 0;
}