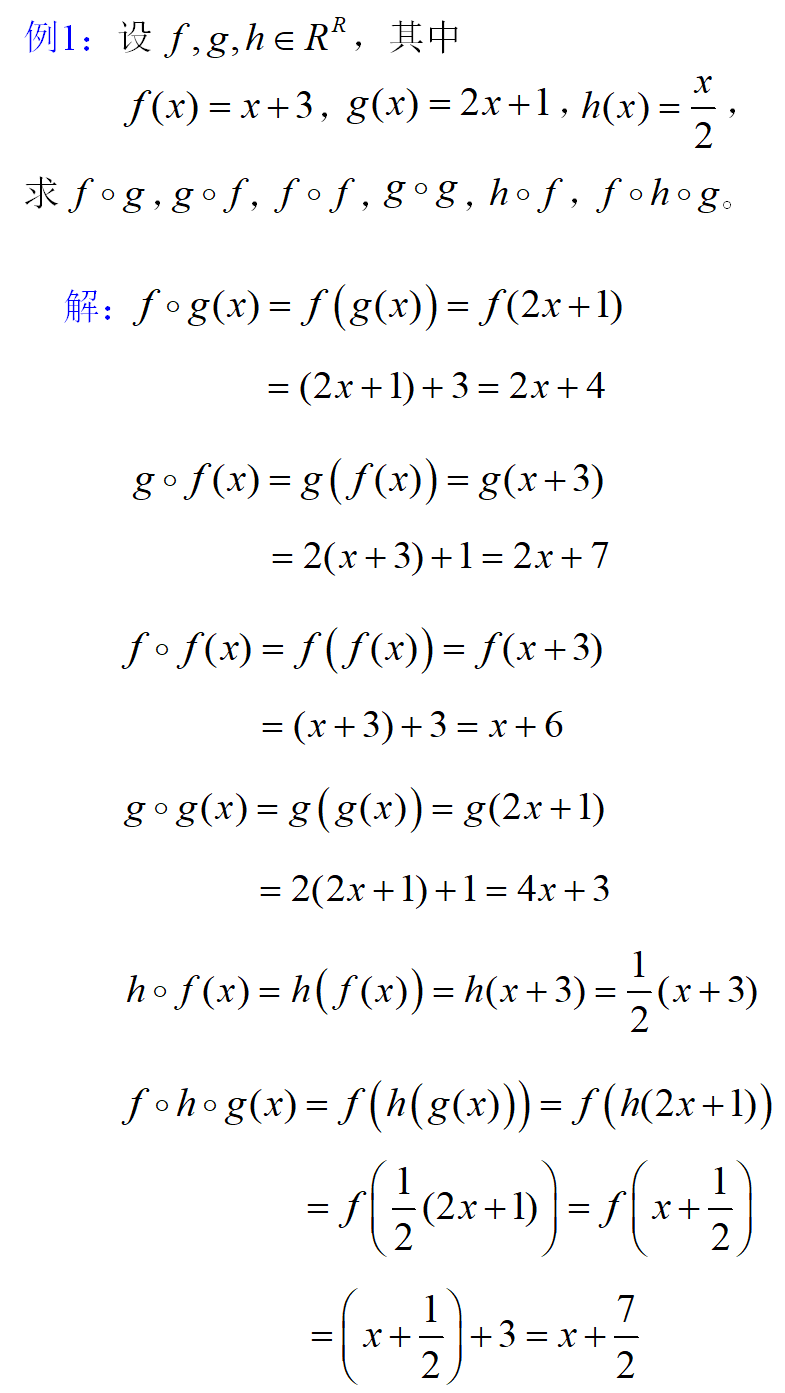151.函数

1.概念

函数是二元关系中特殊的一类，也就是说，函数是一种特定类型的二元关系。本章讨论的是离散函数，它能把一个有穷集合变换到另一个有穷集合。

1.1定义

给定两个集合X和Y，设 f 是从X→Y的一种关系，若对于每一个 x ∈ X，都存在唯一一个 y ∈ Y，使得 x f y，则称关系 f 为函数（映射），并记为：f：X→Y。

例如：是函数

不是函数.

注：⑴ 在函数 f：X→Y中，若 < x, y > ∈ f ，则称 x 为自变量，

与 x 对应的 y 称作 f 作用下的象点（值）；也可用 y = f (x) 表示 x f y 。

⑵ X中每一个元素均有定义，∴函数 f 的定义域 dom f =X.

⑶ f 值域 ran f ⊆ Y，（有时也记为 R_f ）
R_f = { y | ∃x (x ∈ X ) ∧ ( y = f (x)) }
集合 Y称为 f 的陪域。

⑷ 对于某一个 x ∈ X，其值 f(x)是唯一的，即
< x, y > ∈ f ∧ < x, z > ∈ f ⇒ ( y = z)

⑸ 函数是一种特殊的二元关系，所以，有关集合和关系的运算对函数都适合。

 

          

例如：判定下列关系是否为函数

 

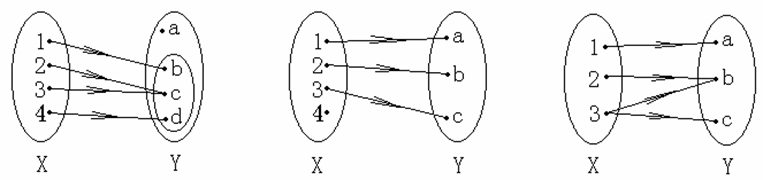
D_f = X  R_f ⊆ Y 是函数          Df ≠ X  不是函数            值不唯一 不是函数

 例如：设X=Y=R（实数）

(1) f = { < x, y >| x, y ∈ R ∧ y = x² }

解：D_f =R， y = x² 的值是唯一的。

(2)g = { < x, y >| x, y ∈ R ∧ x = y² }

解：这不是函数，不满足值的唯一性.

1.2函数的构成

例如：设X={a, b, c}，Y={0, 1}，则

X ×Y = { < a, 0> < a, 1>  < b, 0>  < b, 1>  < c, 0 > < c, 1>  }

显然，在X × Y 中，有2⁶ = 64 个子集，但在这64个子集中只有 2³ = 8 个子集符合函数的定义，这8个函数为：

 

讨论：从此例中可得三点结论：

⑴ 设|X|=m，|Y|=n，则函数 f：X→Y中均是 m个序偶的集合；（即序偶个数=定义域的基数）
⑵ X中每一个元素所对应的象点 f(x)都是Y中的某一个，从而，从X → Y的所有函数个数共
| Y ^X |= n^m =| Y |^|X| 个.

 

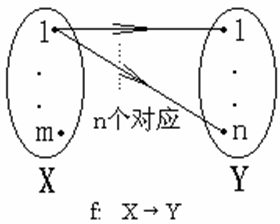
⑶ X→Y有别函数的个数和 X ×Y 子集个数的关系为：
| Y ^X |= n^m << | X × Y | = 2^{m × n} .
即二个集合之间能构成的函数个数比能构成的二元关系个数少得多。

 1.3分类

1.3.1满射函数 

给定函数  f：X→Y，如果值域 R_f  = Y ，则称 f 为满射函数。

 

满射函数一定有：
⑴ |X| ≥ |Y|；
⑵ R_f = Y

1.3.2单射函数

给定函数 f：X→Y，如果有
x₁ ≠ x₂ ⇒ f (x₁) ≠ f (x₂) 或 f (x₁) = f (x₂) ⇒ x₁ = x₂，
则称 f 是单射函数。

 

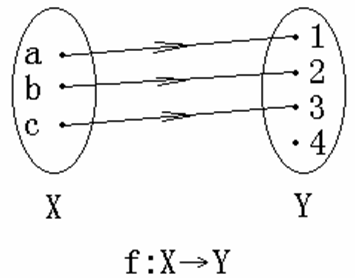
单射函数一定有：
⑴ |X| ≤ |Y|；
⑵ R_f ⊆ Y

1.3.3满射函数

给定函数 f：X→Y，如果 f 既是满射函数，又是单射函数，则称 f 为双射函数。
（“一一对应函数”，“一对一满射函数”）

双射函数一定有：
⑴ |X| = |Y|；
⑵ R_f = Y

例如：在全班同学的集合中，
设 X={序号}，Y={姓名}，
则 f：X→Y是一双射函数。
（序号和姓名的关系）

 2.特殊的

2.1复合函数

定义：复合关系 R◦S = { <x , z> | x∈X∧z∈Z∧∃ y (y∈Y∧x R y∧y S z ) }

定理：给定函数 f ：X→Y 和 g：W→Z，若 f (X) ⊆ W，则称
g ◦ f = { <x , z> | x∈X∧z∈Z∧∃ y (y∈Y∧ y = f (x)∧z = g(y) ) }
为函数 g 与 f 的复合函数。

注： 函数 g ◦ f 称为 g 在 f 的左边可复合。

定理：设 f：X→Y 和 g：Y→Z 是二个函数，于是复合函数 g ◦ f 是一个从 X 到 Z 的函数，对于 ∀ x ∈ X 有：
g ◦ f (x) = g ( f (x) ) .

例如：设X={1, 2, 3}，Y={p , q}，Z={a , b}，
f： X→Y = { <1, p> <2, p> <3, q> }，
g：Y→Z = { <p, b> <q, b> } ，
则：g ◦ f = { < 1, b > < 2, b > < 3, b > }.

显然，g ◦ f 是X→Z的函数。

定理：

设函数 f：X→Y 和 g：Y→Z ，g ◦ f 为复合函数，则：
(1)若 f 和 g都是满射函数，则 g ◦ f 也是满射函数；
(2)若 f 和 g都是单射函数，则 g ◦ f 也是单射函数；
(3)若 f 和 g都是双射函数，则 g ◦ f 也是双射函数.

 

2.2常函数

 给定  f： X→Y，如果对于 ∀ x ∈ X 和某一个 y ∈ Y ，有  f (x) = y，则称  f 为常函数。

 

2.3恒等函数

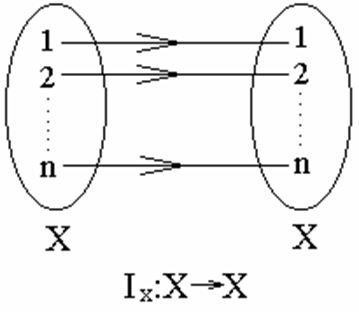
给定 Ix ：X→ X ，若对于 ∀ x ∈ X有 I_x (x) = x，即
I_x = { <x, x >| x ∈ X}，
则称 I_x 为恒等函数

 

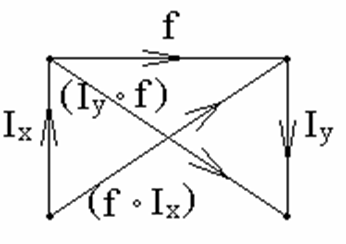
定理：对于任何函数 f ：X→Y，其中
I_x 是X→X的恒等函数，I_y 是Y→Y的恒等函数，
则有 f ◦ I_x = I_y ◦ f = f .

 

 2.4逆函数/反函数

设二元关系 R = { <x , y> | x∈X , y∈Y }，

则R的逆关系 ={ <y , x> | x∈X , y∈Y } .

那么，函数 f 能否像二元关系 R 那样得到逆函数呢？

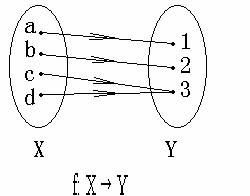
引例：设函数 f：X→Y如图所示

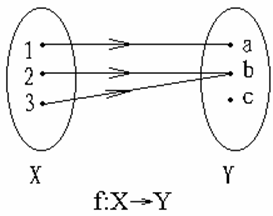
由引例可见：
(1) 逆关系 的定义域不是Y，而是Y的子集；

(2) 逆关系 不满足函数定义：即值是唯一的；所以   是一种二元关系，而不是函数

(3) 如果一个函数的反函数存在的话，则此函数一定是双射函数，

     而单射，满射函数的逆关系均不满足函数的定义；

为了和逆关系相区别，函数 f 的 “逆函数” 用 f ^-1 来表示。

定义：设函数 f：X→Y是一双射函数，
则 f ^-1：Y → X 也是双射函数，且称 f -1 是函数 f 的反函数。

定理：如果函数 f：X→Y有逆函数 f ^-1 ：Y→X，则
f ^-1 ◦ f = I_x 且 f ◦ f ^-1 = I_y .

此定理说明：可用双射函数 f 和 f ^-1 的复合来生成恒等函数。

定理：若  f 是一双射函数，则 ( f ^-1) ^-1 = f .

定理：设函数 f：X→Y 和 g：Y→Z ， 且 f 和 g 均为双射函数，则有
( g ◦ f )-1 = f ^-1 ◦ g ^-1 .