题目描述
zP1nG很清楚自己打不过灭霸,所以只能在自己出的题里欺负他。
咳咳。这一次他得到了空间宝石(Tesseract)。
世界之树连接着九界,此时灭霸和zP1nG都在九界的某个地方。而九界是相互无法到达的。zP1nG为了追杀灭霸,决定使用空间宝石的力量到达灭霸身边。因为zP1nG不擅长使用空间宝石,无法直接开一条从自己的位置到灭霸的位置的传送门,所以他只能无意识地使用空间宝石的力量。zP1nG想知道,在自己胡乱地使用空间宝石后,通过传送门到达灭霸的位置最少需要多长时间。
具体地,九界的编号为0~8,共有(n)道传送门,第i道传送门为优先级为(p_i),由(u_i)到(v_i),需要花费(w_i)个时间的单向门。传送的规则为:zP1nG按顺序穿过的传送门的优先级必须是单调不降的。例如,zP1nG穿过了三道传送门到达灭霸的位置,这三道传送门的优先级分别为1→2→2即为一种合法的方式,而优先级分别为1→2→1是不合法的。
zP1nG会使用(q)次宝石的力量来尝试进行传送:其中第(i)次尝试会打开数道传送门,这些传送门的优先级会形成(s_i)个区间。例如,在某次尝试中zP1nG打开了三个区间([1,2]),([4,7]),([9,10]),那么优先级在这三个区间内的传送门将全部被打开并允许zP1nG穿过。你需要告诉zP1nG在此情况下从自己的位置(z_i)到达灭霸所在处(t_i)所需的最短时间。尝试结束后所有传送门会关闭。
输入格式
第(1)行包含两个正整数(n)和(S),(S)的含义见数据范围与约定所述。
第(2)至(n+1)行每行包含4个正整数(p_i),(u_i),(v_i),(w_i)。
第(n+2)行包含一个正整数(q)。
第(n+3)至第(n+q+2)行每行若干个正整数,其中前三个数为(z_i),(t_i),(s_i),之后为(2 imes si)个正整数,表示每个区间的左右端点。
各变量具体含义见题目描述所述。
输出格式
对于zP1nG进行的每次尝试,输出一行一个数表示从zP1nG的位置到灭霸的位置所需的最短时间,如果zP1nG无法到达灭霸的位置则输出-1。
样例
样例输入
6 2
1 2 4 1
2 1 3 3
3 1 2 2
4 3 4 5
5 2 4 3
6 1 4 2
4
1 4 1 1 3
1 4 1 1 4
1 4 2 5 5 2 3
1 4 1 1 6
样例输出
-1
8
5
2
数据范围与约定
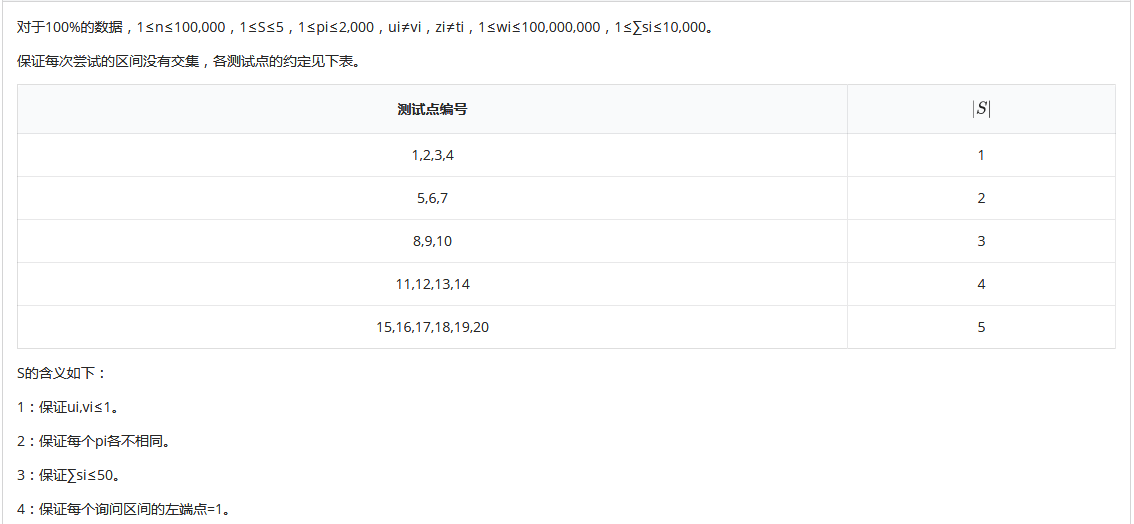
5为无特殊限制
题解
神仙题,考试的时候一头雾水,看着像最短路但总是缺点什么。要知道道路的优先级单凭一次的Dij或Spfa都是无法解决的,因为无论怎么加限制,我们都无法保证在松弛时所做的那一个选择一定是最优的,这点大家可以通过手动模拟数据试验一下。
所以这道题不能用大众的Dij或Spfa来解决。
面对这种限制条件极其恶心,可能情况极其多的类型,最好的办法,那就是把所有情况都算一遍!
那么我们剩下的,也就是只有万年小冷门(其实并没有)的Floyd了!
其实题干中已经说明节点数一共也就有9个,也就是说我们完全可以用联接矩阵来存储整张图,(n^3)的效率完全可以接受,这就给了Floyd操作的空间。而对于优先级的问题,通过研究数据我们知道优先级最多有2000个,在(9^3)的基础上再乘上2000,这样的时空效率我们也是可以接受的。所以我们的办法就是针对每一个优先级都建一个联接矩阵,然后以等级作为区间构建线段树。
没错,你没有看错,就是线段树。鬼知道最短路还能放在线段树上,活久见。
唯一能够有所提示的地方估计就是每次给出的优先级都是区间吧...对优先级建树,每个树节点都有一个矩阵,(dis[i][j]) 代表在当前树节点包含的区间(即优先级区间)内 (i) 到 (j) 的最短路。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
const int maxn = 2000 + 10;
char buf[1 << 20], *p1 = buf, *p2 = buf;
// fread版快读,输入结束后手动输入EOF结束输入
char getc() {
if (p1 == p2) {
p1 = buf;
p2 = buf + fread(buf, 1, 1 << 20, stdin);
if (p1 == p2)
return EOF;
}
return *p1++;
}
inline int read() {
int s = 0, w = 1;
char c = getc();
while (c < '0' || c > '9') {
if (c == '-')
w = -1;
c = getc();
}
while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getc();
return s * w;
}
struct node {
int l, r;
bool operator<(const node& x) const { return l < x.l; }
} q[maxn]; //存储每一个可以打开的区间
struct Maxtrix {
int dis[10][10];
void Init() {
//有点类似于单位矩阵的初始化
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++) dis[i][j] = (i == j ? 0 : 0x3f3f3f3f);
}
} G[maxn]; //为每一个优先级都建一张图
struct tree {
Maxtrix data;
int l, r;
} t[maxn << 2];
inline Maxtrix Update(Maxtrix a, Maxtrix b) {
Maxtrix c;
c.Init();
//标准的floyd最短路 ,又有点像矩阵乘法
for (int k = 0; k < 9; k++)
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++) c.dis[i][j] = min(c.dis[i][j], a.dis[i][k] + b.dis[k][j]);
return c;
}
#define tl t[u].l
#define tr t[u].r
#define ls (u << 1)
#define rs (u << 1 | 1)
void Pushup(int u) { t[u].data = Update(t[ls].data, t[rs].data); }
void Build(int u, int l, int r) {
//每个线段树节点的所代表的区间都是优先级的区间
t[u].l = l;
t[u].r = r;
if (l == r) {
t[u].data = G[l];
return;
}
int mid = (tl + tr) >> 1;
Build(ls, l, mid);
Build(rs, mid + 1, r);
Pushup(u);
}
Maxtrix Ask(int u, int l, int r) {
if (l <= tl && tr <= r) {
return t[u].data;
}
int mid = (tl + tr) >> 1;
bool flag = 0;
Maxtrix ans;
if (l <= mid) {
ans = Ask(ls, l, r);
flag = 1;
}
if (r > mid) {
if (flag)
ans = Update(ans, Ask(rs, l, r));
else
ans = Ask(rs, l, r);
}
return ans;
}
int main() {
int n = read(), S = read();
for (int i = 1; i <= 2001; i++) G[i].Init();
int p, u, v, w;
for (int i = 1; i <= n; i++) {
p = read(), u = read(), v = read(), w = read();
G[p].dis[u][v] = min(G[p].dis[u][v], w);
}
for (register int t = 1; t <= 2001; t++) //事先预处理单独每一级优先级的最短路
for (register int k = 0; k < 9; k++)
for (register int i = 0; i < 9; i++)
for (register int j = 0; j < 9; j++)
G[t].dis[i][j] = min(G[t].dis[i][j], G[t].dis[i][k] + G[t].dis[k][j]);
//线段树主要是解决涉及多个优先级的最短路
//按照优先级作为区间构造线段树,每一个区间内的树节点所记录的数据,就是每一个优先级区间内所能达到的最短路
Build(1, 1, 2001);
int cas = read();
int st, ed, siz;
while (cas--) {
st = read(), ed = read(), siz = read();
for (register int i = 1; i <= siz; i++) //读入每个可使用的优先级区间
q[i].l = read(), q[i].r = read();
sort(q + 1, q + 1 + siz);
Maxtrix ans = Ask(1, q[1].l, q[1].r); //我们按照优先级作为区间构造了线段树,更新答案时直接在相应的区间内查询即可
for (register int i = 2; i <= siz; i++) {
ans = Update(ans, Ask(1, q[i].l, q[i].r));
}
printf("%d
", (ans.dis[st][ed] == 0x3f3f3f3f ? -1 : ans.dis[st][ed]));
}
}