组合和排序
(假如有同学不小心进来了,那也没事,博是给我自己写的,但你们千万不要笑我,认真!)
组合和排序是OI学生们的基本功,其重要性不言而喻。(而我认为它的最大作用就是解决生物的遗传问题!)
这注定是一个废掉的下午,顶着同学们都在打假期题的危机,我开始一个人神游。
、( - A - )、
基本定义:
感受着互联网带我们的便捷,于是我就转了百度百科。
组合数(combinatorial number):
从m个不同元素中,任取n(n≤m)个元素并成一组,叫做从m个不同元素中取出n个元素的一个组合;从m个不同元素中取出n(n≤m)个元素的所有组合的个数,叫做从m个不同元素中取出n个元素的组合数。
套路上说,鉴于人们对用数学描摹一切未知事物的热情,于是一个可爱的公式出现了。
组合数计算公式:
最基本的有:

特别的有,c(n,0)=1(这个其实也和后面的拓展有关系)
接着是拓展:
C(n,m)= C(n,n-m)= C(n-1,m-1)+C(n-1,m)
怎么理解这个公式?(因为我给不了证明啊)
首先:
C(n,m)= C(n,n-m)
这个公式好说,既然我们确定确定一种组合的组合数(c(n,m)),另一种组合数也就固定了。(补集思想!)
但:
C(n,m)= C(n-1,m-1)+C(n-1,m)
显然,这是一个递推式,但这个就有点麻烦了。
于是机智的我翻到了一种理解方式:
现在我们有n+1个球,我们从里面选m个。 这个我们知道共有C(m,n+1)种选法。
然后我们在这n+1个球里随便挑一个,叫它a球。
那么在这C(m,n+1)种选法里就分成了两类,且只有这两类。
一类是选出来的m个球里没有a球。 这类选法数量等价于n个球里选m个,就是C(m,n) 还有一类是选出来的m个球里有a球。
这类选法数量等价于n个球里选m-1个,就是C(m-1,n)
这下是不是好记多了?
排序数(Arrangement number):
从n个不同元素中任取r(r≦n)个元素排成一列(考虑元素先后出现次序)称此为一个排列,此种排列的总数即为排列数,即叫做从n个不同元素中取出r个元素的排列数。
又是套路。
排序数计算公式:
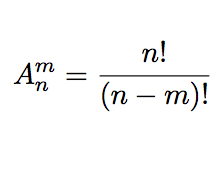
排序貌似没什么好说的?
排序数和组合数的关系:
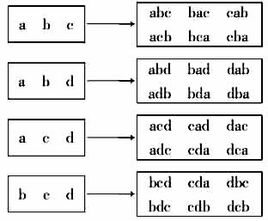
还记得上面的那个两个基本公式么,看看这张图,是不是明白排序数的公式是怎么来的了?(其实就是在原来的组合数公式上*A(n,n),也就是*n!)
还有一些话:
这次noip有个interesting的题:组合数问题,但和这个组合数公式并无太大关系。
真的要算组合数,那就直接拿原式即可。
如果你还想取模,那就找 this 。
动态规划,杨辉三角...怎么想好像都不妥。
二项式定理:
大概作用是结合组合解开二项多次式吧。
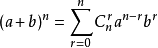
这个我真的不会!但他却带来了一个公式
C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2^n
结合二项式定理,让此式中让(a,b)都为1即可。
2017.6.6_16:42:16 : 大部分内容待补,今天先跑(还有生物题!)。