142. Linked List Cycle II【easy】

142. Linked List Cycle II【easy】

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Note: Do not modify the linked list.

Follow up:
Can you solve it without using extra space?

解法一：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == NULL || head->next == NULL) {
            return NULL;
        }
        
        ListNode * slow = head;
        ListNode * fast = head;
        
        while (fast->next != NULL && fast->next->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            
            if (fast == slow) {
                return findNode(fast, head);
            }
        }
        
        return NULL;
    }
    
    ListNode * findNode(ListNode * fast, ListNode * head)
    {
        while (fast != head) {
            fast = fast->next;
            head = head->next;
        }
        
        return head;
    }
    
    
};

首先先看是否有环，有环的话我们要把其中一个指针移动到链表head节点，另外一个指针不变，然后这两个指针同时往前分别走一步，直到相等为止就是环的入口点；这个问题的算法证明如下：

 问题1：如何判断单链表中是否存在环（即下图中从结点E到结点R组成的环）？

        设一快一慢两个指针（Node *fast, *low）同时从链表起点开始遍历，其中快指针每次移动长度为2，慢指针则为1。则若无环，开始遍历之后fast不可能与low重合，且fast或fast->next最终必然到达NULL；若有环，则fast必然不迟于low先进入环，且由于fast移动步长为2，low移动步长为1，则在low进入环后继续绕环遍历一周之前fast必然能与low重合（且必然是第一次重合）。于是函数可写如下：

bool hasCircle(Node* head, Node* &encounter)  
{  
    Node *fast = head, *slow = head;  
    while(fast && fast->next)  
    {  
        fast = fast->next->next;  
        slow = slow->next;  
        if(fast == slow)  
        {  
            encounter = fast;  
            return true;  
        }  
    }  
    encounter = NULL;  
    return false;  
}  

 问题2：若存在环，如何找到环的入口点（即上图中的结点E）？
       解答：如图中所示，设链起点到环入口点间的距离为x，环入口点到问题1中fast与low重合点的距离为y，又设在fast与low重合时fast已绕环n周（n>0），且此时low移动总长度为s，则fast移动总长度为2s，环的长度为r。则
        s + nr = 2s,n>0      ①
        s = x + y               ②
       由①式得  s = nr                 
       代入②式得
       nr = x + y
       x = nr - y                ③
       现让一指针p1从链表起点处开始遍历，指针p2从encounter处开始遍历，且p1和p2移动步长均为1。则当p1移动x步即到达环的入口点，由③式可知，此时p2也已移动x步即nr - y步。由于p2是从encounter处开始移动，故p2移动nr步是移回到了encounter处，再退y步则是到了环的入口点。也即，当p1移动x步第一次到达环的入口点时，p2也恰好到达了该入口点。于是函数可写如下：

Node* findEntry(Node* head, Node* encounter)  
{   
    Node *p1 = head, *p2 = encounter;  
    while(p1 != p2)  
    {  
        p1 = p1->next;  
        p2 = p2->next;  
    }  
    return p1;  
}  

另外一个解释也比较好：

求解单链表环入口点的步骤：

1：使用“指针追赶”方法找到相遇点（网上资料很多，此处略）。

2：指针p1从链表头、p2从相遇点，同时出发，一次移动一个节点，再次的相遇点便是环的入口点。

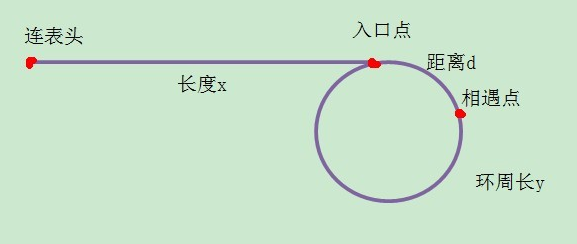
证明导向：p1从表头走，能与p2从相遇点走再次相遇，那么说明p1走到入口点时，p2可能刚好走了y-d（其中d是入口点与第一次相遇点的距离）个节点，或者走了几圈再加上y-d个节点。故就要找到y-d与x的关系。

第一次相遇：S慢：表示一次移动一个节点的指针所走的路程（即节点个数）

                  S快：表示一次移动两个节点的指针所走的路程（节点个数）

            S慢 = x + d

            S快 = 2（x + d）

            S快 - S慢 = n倍y

            则有：x + d = ny

                  x = ny - d = （n - 1）y + （y - d）

    由此便说明了：x 个节点就相当于（n - 1）倍环周长加上y - d，正好是第一次相遇点到入口点的距离。

证明参考自：

http://blog.csdn.net/wuzhekai1985/article/details/6725263

http://blog.sina.com.cn/s/blog_6a0e04380101a9o2.html