题目已经写的很清楚是最短路问题了,但是这是一个考几何的最短路emmm,所以我把他放来综合题。
题意:给出两条平行线跟n个圆,然后在圆上走跟在线上走不消耗体力,求L1到L2的最短路
首先写这道题需要反复用这两个公式

平行线距离公式
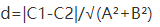
我们很容易就能想到把整个圆看成一个点,然后去做最短路,那么我们就要加一个源点跟汇点,源点为L1,汇点为L2
然后枚举算出所有圆到源点跟汇点的距离。再枚举算出在圆与圆之间的最短路。
然后就可以开始我们愉快的dijstra了
代码如下:
#include <bits/stdc++.h> using namespace std; #define ll long long #define re register #define P pair<int,int> #define mp make_pair #define pb push_back #define fi first #define se second const int N=1e6+10; const int mod=19260817; void read(int &a) { a=0; int d=1; char ch; while(ch=getchar(),ch>'9'||ch<'0') if(ch=='-') d=-1; a=ch-'0'; while(ch=getchar(),ch>='0'&&ch<='9') a=a*10+ch-'0'; a*=d; } void write(int x) { if(x<0) putchar(45),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); } struct note { int pos; double dis; bool operator < (const note &x) const { return x.dis<dis; } }; int a[1005][5],n; double l[1005][1005],dis[1005]; bool vis[1005]; priority_queue <note> q; inline void dijstra(int st) { memset(dis,126,sizeof(dis)); dis[st]=0.0; q.push({st,0.0}); while(!q.empty()) { note x=q.top(); q.pop(); if(vis[x.pos]) continue; vis[x.pos]=1; for(re int i=0;i<n+2;i++) { if(dis[i]>x.dis+l[x.pos][i]) dis[i]=x.dis+l[x.pos][i],q.push({i,dis[i]}); } } } int main() { int A,B,C1,C2; read(n); read(A); read(B); read(C1); read(C2); for(re int i=0;i<n;i++) for(re int j=0;j<=2;j++) read(a[i][j]); int s=n,t=n+1; l[s][t]=l[t][s]=1.0*abs(C1-C2)/sqrt(((double)A*A+(double)B*B)); for(re int i=0;i<n;i++) { l[s][i]=l[i][s]=max(0.0,1.0*abs((A*a[i][0]+B*a[i][1]+C1)/sqrt((double)A*A+(double)B*B))-a[i][2]); l[t][i]=l[i][t]=max(0.0,1.0*abs((A*a[i][0]+B*a[i][1]+C2)/sqrt((double)A*A+(double)B*B))-a[i][2]); } for(re int i=0;i<n;i++) for(re int j=0;j<n;j++) if(i!=j) l[i][j]=l[j][i]=max(0.0,1.0*sqrt((a[i][0]-a[j][0])*(a[i][0]-a[j][0])+(a[i][1]-a[j][1])*(a[i][1]-a[j][1]))-a[i][2]-a[j][2]); dijstra(s); cout<<dis[t]<<endl; return 0; }