P2495 [SDOI2011]消耗战

 题意

给一棵树，1是根；

然后树上有M个资源站，现在要求你断开一些边，让根连不到所有的资源站，

考虑显然o（n）的树DP

但是有M次询问 复杂度nm

然后我们发现ki的加和比较小

然后建立虚树，每次只处理ki个点就行了

然后虚树怎么建立，我们发现只需要包含这ki个点，和他们的lca就可以了；

----------------------------------------------------------------------------------------以下内容转自 洛谷题解：https://www.luogu.com.cn/blog/Tian2837601005/solution-p2495 （侵权删）

那么，在虚树上应该保留原树上的哪些点呢？

首先，每次讯问中给出的 kk 个关键点（资源丰富的岛屿）显然应该包含在虚树中。其次，任意两个关键点的最近公共祖先也应该包含在虚树中；因为在本题中，切断一条边可以同时切断根节点与多个关键点间的路径，最近公共祖先的存在为动态规划提供了这种状态转移。最后为了方便，我们可以将 11 号节点（即根节点）也加入到虚树中。

构造虚树的方法很多，在这里介绍一种用栈建树的算法流程。

令 11 号节点为虚树的根。

将所有关键点按照其在原树中的 dfs 序升序排序。假设当前正在处理的关键点为 uu 。

维护一个栈，使得栈底到栈顶的元素依次为虚树上从根节点到节点 uu 的一条链。

这里为什么要维护一个栈呢？

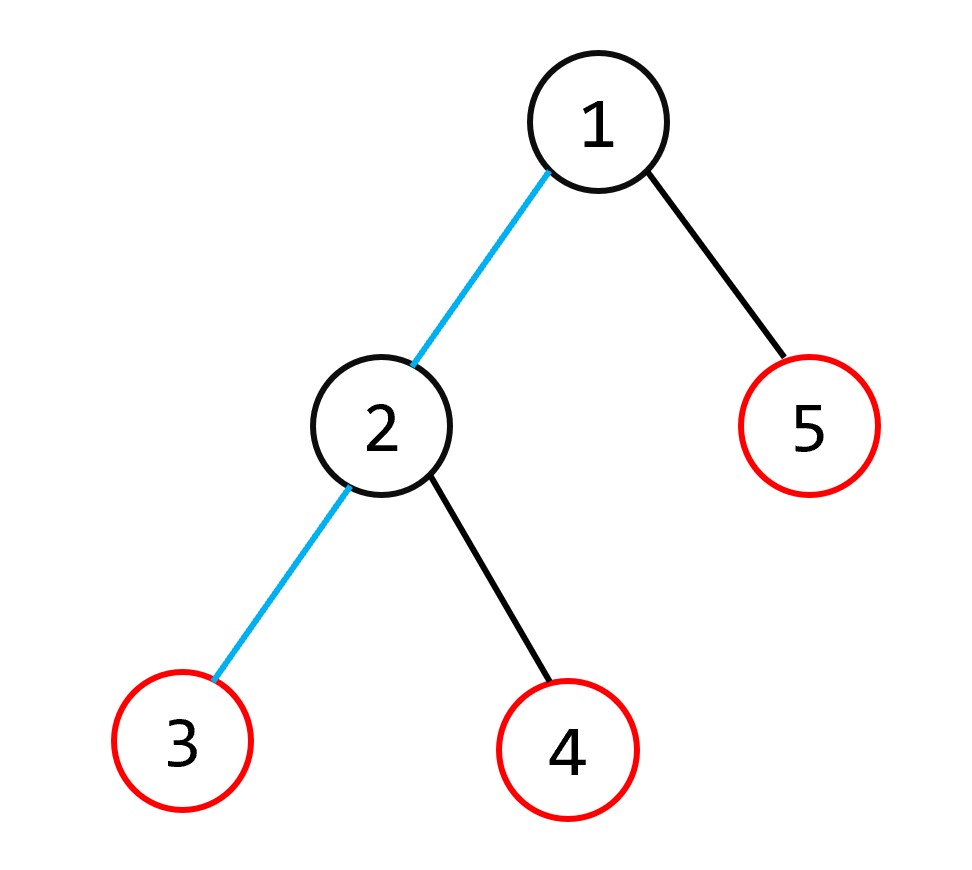
如图：在处理完 33 号关键点后，虚树中只有 11 、 33 两个节点，栈中的元素依次为 11 、 33 。但是这条链是不完整的，可以观察到在处理 44 号关键点时，还需要将 22 号节点添加到虚树中。利用栈的性质，我们可以动态维护一条虚树上的链，并在必要的时候添加节点。

回到刚才的叙述，当前正在处理关键点 uu 。根据栈的定义，上一个处理的关键点一定为 stack.top()stack.top() 。

由于进行过排序，即节点 uu 的 dfs 序大于上一个关键点的 dfs 序，因此节点 uu 要么是上一个关键点的后代，要么与其没有祖先-后代的关系。

显然，如果节点 uu 是 stack.top()stack.top() 的后代，那么只需将节点 uu 入栈即可，因为 uu 在虚树中，一定是上一个关键点的儿子。

但是如果节点 uu 与 stack.top()stack.top() 没有祖先-后代的关系，那么此时的讨论将比较复杂。

可以结合上图观察，假设当前正在处理 44 号关键点。我们可以首先将栈顶弹出，因为 stack.top()stack.top() 一定不在根节点到节点 uu 的链上。此时，栈中剩余的元素只有 11 。然而， 33 与 44 的最近公共祖先 22 号节点还不在栈中；因此我们需要把 22 号节点入栈，并将刚刚弹出的节点与新的栈顶在虚树中连边。处理结束后，将 44 入栈。

接下来处理 55 号关键点，此时栈中的元素依次为 11 、22 、44 。首先将栈顶弹出，但由于我们接下来需要维护的链为 1->51−>5 ，栈中仍然有节点 22 ，因此我们需要将 22 和刚刚弹出的节点 44 连边，并且重复以上操作。将新的栈顶 22 弹出后，栈中只剩下节点 11 。这时发现 11 号节点恰好为 55 与上一次处理的关键点 44 的最近公共祖先，因此将 11 与 22 连边后，弹栈可以中止了。处理结束后，将 55 入栈。

此时我们已经处理完了所有关键点，但是栈中的元素间还没有连边。将栈中的节点依次连边后，虚树的构建就完成了。

-------------------------------------------------------------------------------以上内容转自 洛谷题解：https://www.luogu.com.cn/blog/Tian2837601005/solution-p2495 （侵权删）

我们发现每次个点最多加入一个lca，所以虚树最后的点最多是2*ki 保证了复杂度

设ki的加合为k，总复杂度为o（klogk）   （其实是klogn+klogk+n+klogn+.................）其中klogk数量级最大

以下代码同样参考上述博客，只是带本人风格写了一下，通过上述大佬的博客学了很多代码细节

#include<bits/stdc++.h>
#define pb push_back
#define fi first
#define se second
#define io std::ios::sync_with_stdio(false)
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const double pi=acos(-1);
const ll P = 998244353, INF = 0x3f3f3f3f;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll qpow(ll a,ll n){ll r=1%P;for (a%=P; n; a=a*a%P,n>>=1)if(n&1)r=r*a%P;return r;}
const double eps=1e-5;
const ll maxn=3e5+10;
ll lcm(ll a,ll b){return a*b/gcd(a,b);}
ll pos[maxn];
ll head[maxn],_next[2*maxn],to[2*maxn],w[2*maxn];
ll cnt,tot;
void add(ll x,ll y,ll ww)
{
   cnt++,_next[cnt]=head[x],head[x]=cnt,to[cnt]=y,w[cnt]=ww;
   cnt++,_next[cnt]=head[y],head[y]=cnt,to[cnt]=x;w[cnt]=ww;
}
ll lg[maxn];
ll stak[maxn],top;
ll f[maxn][20],g[maxn][20];
ll ff[maxn];
ll dep[maxn];
ll st[maxn],h[maxn];
struct edg
{
    ll to;
    ll w;
    edg();
    edg(ll t,ll ww)
    {
      to=t;
      w=ww;
    }
};
vector<edg> ed[maxn];
void dfs(ll u,ll fa)
{
   pos[u]=++tot;
   f[u][0]=fa;
   ff[u]=fa;
   dep[u]=dep[fa]+1;
   for(ll i=1;(1<<i)<=dep[u];i++){
   f[u][i]=f[f[u][i-1]][i-1];
   g[u][i]=min(g[f[u][i-1]][i-1],g[u][i-1]);//预处理最短距离
 }
  for(ll i=head[u];i;i=_next[i])
  {
    ll v=to[i];
    if(v==fa) continue;
    g[v][0]=w[i];
    dfs(v,u);
  }
}
ll lca(ll x,ll y)
{
    if(dep[x]<dep[y])swap(x,y);
    for(ll i=19;i>=0;i--)
        if(dep[f[x][i]]>=dep[y])x=f[x][i];
        if(x==y)return x;
    }
    for(ll i=19;i>=0;i--)
    {
        if(f[x][i]!=f[y][i])
        {
            x=f[x][i];y=f[y][i];
        } 
    } 
    return f[x][0];
}
void addedg(ll x,ll y)
{
   ll ans=INF;
   ll xx=y;
   while(dep[y]>dep[x])  //学了一波细节操作，快速求两点之间的最短的那条边
    {
      ans=min(ans,g[y][lg[dep[y]-dep[x]]]);
      y=f[y][lg[dep[y]-dep[x]]];
    }
    ed[x].push_back(edg(xx,ans));
}
void dp(ll u){  //dp操作
  for(auto x:ed[u])
   {
      ll v=x.to;
      ll w=x.w;
      dp(v);
      if(st[v])h[u]+=w;
      else h[u]+=min(w,h[v]);
      st[v]=0;h[v]=0;
  }
  ed[u].clear();
}
bool cmp(ll x,ll y)
{
  return pos[x]<pos[y];
}
int main()
{ io;
  for(ll i=0;i<20;i++)g[1][i]=INF;
  for(ll i=2;i<maxn;i++)lg[i]=lg[i>>1]+1;//预处理log
  ll n;
  cin>>n;
  for(ll i=1;i<n;i++)
  {
    ll x,y,ww;
    cin>>x>>y>>ww;
    add(x,y,ww);
  }
  dfs(1,0);
   ll q;
   cin>>q;
   while(q--)
   {
     ll k;
     cin>>k;
     vector<ll> s;
     for(ll i=1;i<=k;i++)
     {
      ll x;
      cin>>x;
      st[x]=1;
      s.push_back(x);
     }
    sort(s.begin(),s.end(),cmp);//按DFS序排序
     stack<ll> st;
      st.push(1);
        for (auto u:s) {    //建虚树
            ll l = lca(u, st.top());
    
            while (st.top() != l) {
                ll tmp = st.top(); st.pop();
                if(pos[st.top()]<pos[l])
                {
                  st.push(l);
                }
                addedg(st.top(), tmp);
            }
            st.push(u);
        }
        while (st.top() != 1) {
            ll tmp = st.top(); st.pop();
           addedg(st.top(), tmp);
        }     
     dp(1);
     cout<<h[1]<<endl;
     h[1]=0;
  }
}