
题解
我们发现这个是带修改的,显然点分治做不了,
然后这个是个动态点分治,俗称点分树,暂时没看懂,以后补 ,(大概是,只维护分治时的fa一路更新上去。)
然后有一个比较稳定的括号序列做法(比点分树快。)
括号序列可以快速求一个树上两点之间距离
-------------------以下资料转自洛谷大佬博客 :https://www.luogu.com.cn/blog/user13183/solution-p2056(侵权删)
写个括号序列的做法。
首先dfs整棵树一遍,进入一个节点的时候加上一个左括号,然后是节点编号,当这个节点的所有子树遍历完后再添上一个右括号,这就是括号序列。(其实就是dfs序加上了括号而已)
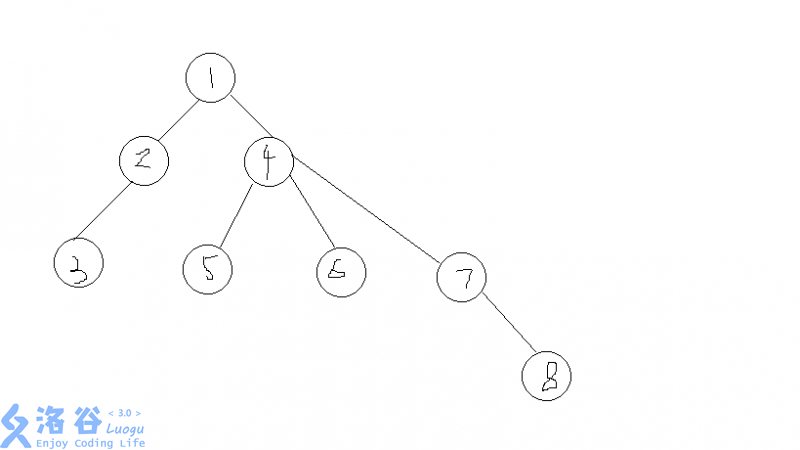
举个栗子,这棵树的括号序列是(1(2(3))(4(5)(6)(7(8))))
我们要求3到8的距离,截取两点间的括号序列为
3))(4(5)(6)(7(8
把编号和匹配的括号删掉
))(((
剩下了5个左右括号,而这就是3到8的距离。
这就是括号序列的性质。
-------------------以上资料转自洛谷大佬博客 :https://www.luogu.com.cn/blog/user13183/solution-p2056(侵权删)
然后具体证明可以见上述网址大佬博客
然后先DFS一下,把树拉成线性 ,用线段树维护左右括号合并就行了,然后中间我们要维护左右括号的几个特殊值
//括号序列 #include<cstdio> //(a1 b1)(a2 b2)->(a,b) //a+b=a1+abs(b1-a2)+b2=max((a1-b1)+(a2+b2),(a1+b1)+(b2-a2)) //需要左区间后缀的max(a-b),max(a+b),右区间前缀的max(a+b),max(b-a) int num,s[300005],pos[1000005],head[100005],n,m,cnt,tot; bool c[100005]; struct edge{int to,next;}e[200005]; void add(int u,int v){e[++num]=(edge){v,head[u]},head[u]=num;} struct node { int a,b,l1,l2,r1,r2,dis; //a,b右左括号数,l1,l2前缀的max(a+b),max(b-a),r1,r2后缀的max(a+b),max(a-b) }tr[1200005]; void dfs(int u,int fa) { s[++tot]=-1;//左括号 s[++tot]=u;pos[u]=tot; for(int i=head[u];i;i=e[i].next) { int v=e[i].to;if(v==fa)continue; dfs(v,u); } s[++tot]=-2;//右括号 } void push(int id,int x) { tr[id].a=tr[id].b=0;tr[id].l1=tr[id].l2=tr[id].r1=tr[id].r2=tr[id].dis=-1e9; if(s[x]==-1)tr[id].b=1;else if(s[x]==-2)tr[id].a=1;else if(!c[s[x]])tr[id].l1=tr[id].r1=tr[id].r2=tr[id].l2=0;//黑点 } int max(int a,int b){return a>b?a:b;} void merge(int id) { int lc=id<<1,rc=id<<1|1; if(tr[lc].b>tr[rc].a) tr[id].a=tr[lc].a,tr[id].b=tr[lc].b-tr[rc].a+tr[rc].b;else tr[id].a=tr[lc].a+tr[rc].a-tr[lc].b,tr[id].b=tr[rc].b; tr[id].l1=max(tr[lc].l1,max(tr[rc].l1+tr[lc].a-tr[lc].b,tr[rc].l2+tr[lc].a+tr[lc].b)); tr[id].l2=max(tr[lc].l2,tr[rc].l2-tr[lc].a+tr[lc].b); tr[id].r1=max(tr[rc].r1,max(tr[lc].r1-tr[rc].a+tr[rc].b,tr[lc].r2+tr[rc].a+tr[rc].b)); tr[id].r2=max(tr[rc].r2,tr[lc].r2+tr[rc].a-tr[rc].b); tr[id].dis=max(max(tr[lc].r1+tr[rc].l2,tr[lc].r2+tr[rc].l1),max(tr[lc].dis,tr[rc].dis)); } void build(int id,int l,int r) { if(l==r){push(id,l);return;} int mid=l+r>>1; build(id<<1,l,mid);build(id<<1|1,mid+1,r); merge(id); } void modify(int id,int l,int r,int x) { if(l==r){push(id,l);return;} int mid=l+r>>1; if(x<=mid)modify(id<<1,l,mid,x);else modify(id<<1|1,mid+1,r,x); merge(id); } int main() { scanf("%d",&n); for(int i=1,u,v;i<n;i++) { scanf("%d%d",&u,&v); add(u,v),add(v,u); } dfs(1,0);cnt=n; build(1,1,tot); scanf("%d",&m); for(int i=1,x;i<=m;i++) { char s[2]; scanf("%s",s); if(s[0]=='C')scanf("%d",&x),cnt+=c[x]?1:-1,c[x]^=1,modify(1,1,tot,pos[x]); else if(cnt==0)printf("-1 ");else if(cnt==1)printf("0 ");else printf("%d ",tr[1].dis); } }