数学：阶和原根

设m > 1 且 gcd(a, m) = 1

那么，使得

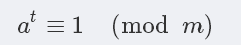
成立的最小正整数t就称之为

a对模m的阶, 记为δm(a)

若δm(a)=ϕ(m), 则称a为m的一个原根

这样一来，和欧拉函数和欧拉定理就有一腿了

关于原根的性质和推论

详见dalao的博客

https://blog.csdn.net/a27038/article/details/77203892

如果g是P的原根，那么g的（1...P-1）次幂mod P的结果一定互不相同

如果p有原根，则它恰有φ(φ(p))个不同的原根

p为素数，当然φ(p)=p-1,因此就有φ(p-1)个原根

POJ1284，求原根个数

当然这只是一个简单的性质

求原根的题还得补

#include<cstdio>
int euler(int n)
{
    int ret=n;
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
        {
            n/=i;
            ret=ret-ret/i;
            while(n%i==0) n=n/i;
        }
    if(n>1) ret=ret-ret/n;
    return ret;
}
int main()
{
    int p;
    while(scanf("%d",&p)==1) printf("%d
",euler(p-1));
    return 0;
}