POJ1186 方程的解数
题目连接:http://poj.org/problem?id=1186
Description
已知一个n元高次方程:
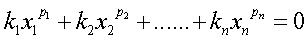
其中:x1, x2,...,xn是未知数,k1,k2,...,kn是系数,p1,p2,...pn是指数。且方程中的所有数均为整数。
假设未知数1 <= xi <= M, i=1,,,n,求这个方程的整数解的个数。
1 <= n <= 6;1 <= M <= 150。
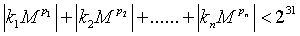
方程的整数解的个数小于231。
★本题中,指数Pi(i=1,2,...,n)均为正整数。
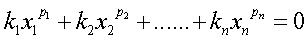
其中:x1, x2,...,xn是未知数,k1,k2,...,kn是系数,p1,p2,...pn是指数。且方程中的所有数均为整数。
假设未知数1 <= xi <= M, i=1,,,n,求这个方程的整数解的个数。
1 <= n <= 6;1 <= M <= 150。
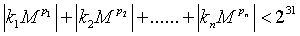
方程的整数解的个数小于231。
★本题中,指数Pi(i=1,2,...,n)均为正整数。
Input
第1行包含一个整数n。第2行包含一个整数M。第3行到第n+2行,每行包含两个整数,分别表示ki和pi。两个整数之间用一个空格隔开。第3行的数据对应i=1,第n+2行的数据对应i=n。
Output
仅一行,包含一个整数,表示方程的整数解的个数。
Sample Input
3
150
1 2
-1 2
1 2
Sample Output
178
Source
Noi 01
分析:
这道题如果暴力枚举的话很显然会超时
150 ^ 6 = 11390625000000.......
150 ^ 3 = 3375000,这是可以接受的
所以我们把方程分成两半,先搜索计算前一半,用hash将所有总值存储起来,再搜索后一半,然后看是否和左值相等,如果相等则是同一个解
解法一:hash + 乘法原理
解法二:存<结果,解数>二元组数组, 双指针扫描 + 乘法原理
时间复杂度都是O(M ^ (n/2) + M ^ (n/2))
这里提供解法一的代码
代码实现:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 6 using namespace std; 7 //#define DEBUG(x) cerr << #x << "=" << x << endl 8 const int hashlen = 1000023; 9 const int maxnodenum = 4000024; 10 11 inline int read() 12 { 13 char ch, c; 14 int res; 15 while (ch = getchar(), ch < '0' || ch < '9') c = ch; 16 res = ch - 48; 17 while (ch = getchar(), ch >= '0' && ch <= '9') 18 res = (res << 3) + (res << 1) + ch - 48; 19 if (c == '-') res = -res; 20 return res; 21 } 22 23 void write(int x) 24 { 25 if (x < 0) putchar('-'), x = -x; 26 if (x > 9) write(x / 10); 27 putchar(x % 10 + '0'); 28 return; 29 } 30 31 int n, m, ans, e, tag; 32 int k[32], p[32]; 33 int head[hashlen + 10]; 34 35 struct node 36 { 37 int val; 38 int cnt; 39 int nxt; 40 }edge[maxnodenum + 10]; 41 42 int hash_value(int x) 43 { 44 return x > 0 ? x % hashlen : x % hashlen + hashlen; 45 } 46 47 void insert(int x) 48 { 49 int y = hash_value(x); 50 for (int i = head[y]; i != -1; i = edge[i].nxt) 51 { 52 if (edge[i].val == x) 53 { 54 ++edge[i].cnt; 55 return; 56 } 57 } 58 edge[e].val = x, edge[e].cnt = 1; edge[e].nxt = head[y], head[y] = e++; 59 } 60 61 int lookup (int x) 62 { 63 int y = hash_value(x); 64 for (int i = head[y]; i != -1; i = edge[i].nxt) 65 if (edge[i].val == x) 66 return edge[i].cnt; 67 return 0; 68 } 69 70 void dfs(int cur, int end, int sum) 71 { 72 if (cur == end) 73 { 74 if (tag == 0) 75 insert(sum); 76 else 77 ans += lookup(-sum); 78 return; 79 } 80 for (int i = 1; i <= m; ++i) 81 { 82 int t = 1; 83 for (int j = 0; j < p[cur]; ++j) 84 t *= i; 85 dfs(cur + 1, end, sum + k[cur] * t); 86 } 87 } 88 89 int main() 90 { 91 n = read(); 92 m = read(); 93 memset(head, -1, sizeof(head)); 94 ans = e = 0; 95 for (int i = 0; i < n; ++i) 96 { 97 k[i] = read(); 98 p[i] = read(); 99 } 100 tag = 0; 101 dfs(0, n /2, 0); 102 tag = 1; 103 dfs(n / 2, n, 0); 104 write(ans); 105 return 0; 106 }
国庆集训完后我就变得大括号换行了qwq...
下一篇博客会写一下窝的代码风格qwq