斜率优化DP是一种DP的一种优化方式,目的在于将一类具有单调性的DP优化为线性。
注:本文只适用于较为基础的斜率优化DP,以便为初学者提供一个思路。这一类可以利用单调性线性或(log)复杂度之内求解的DP问题统称为1D/1D类型的动态规划。
斜率优化DP一般适用于的式子形式为[DP[i]=a[j]+b(i,j)+c]
(a[j])表示一个只与j有关的常量,(b(i,j)) 表示一个与i,j同时有关的量,(c)是一个自带的常量,与i和DP方程自带的常量有关。
由于直接看式子会比较抽象,我们下面来看一道例题
例题
题目:[Usaco2008 Mar]土地购买
农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3×5的地和一块5×3的地,则他需要付5×5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
输入
第1行: 一个数: N
第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽
输出
第一行: 最小的可行费用.
输入样例
500
输出样例
4
100 1
15 15
20 5
1 100
样例提示
FJ分3组买这些土地: 第一组:100×1, 第二组1×100, 第三组20×5 和 15×15 plot. 每组的价格分别为100,100,300, 总共500.
解析
这道题的DP方程是显然的,设(x)为长,(y)为宽。
由于对于一对(i),(j),当(x[i]>x[j])且(y[i]>y[j])时,我们买土地(i)就一定可以把土地(j)顺带买了,所以我们可把这些土地(j)找出来舍去,在DP时无需考虑
于是我们可以对土地按照(x)作为第一关键字,(y)作为第二关键字按递增顺序排序,然后遍历一遍数组,去掉以上所述的一类没有意义的土地(j),这时我们得到了一组按顺序排好的土地,保证(x)递增,(y)递减。
这时我们得到了我们的DP方程,设(f[i])表示前(i)个土地分好组,总共需要的最小代价。即(f[i]=min(f[j]+y[j+1]x[i])),我们对于每一个(i),枚举前面每一个(j)作为决策点,这样我们得到了一个最坏(O(n^2))的方法,这样显然是跑不过的。
这时,我们需要利用这个式子的单调性进行优化。
Part 1
设(k< j< i),(j)、(k)为两个可行的决策点,(i)为DP当前枚举到的土地。这时,我们在(i)处进行决策,考虑在什么情况下,决策点为(j)比决策点为(k)更优(当然,你也可以讨论决策点为(k)比决策点为(j)更优,但是到最后你会发现我们DP的顺序决定了我们选择决策点的顺序)
这时[f[j]+y[j+1]x[i] < f[k]+y[k+1]x[i]]
我们对这个式子进行移项化简[f[j]-f[k] < -x[i](y[j+1]-y[k+1])]
由于(y)具有单调减的单调性(注意每一次用到单调性,这是斜率优化之所以可行的核心),(y[j+1]-y[k+1] < 0),所以这个式子的最终形式是[frac{f[j]-f[k]}{y[j+1]-y[k+1]} > -x[i]]
我们会发现以上的式子非常像一个斜率的计算,所以我们可以把每一个决策点x看作一个点((y[x+1],f[x])),我们比较两个决策点谁更优就是在比较两个点之间的连线的斜率与当前点(i)的(-x[i])。
所以,在(k)、(j)连线的斜率大于(-x[i])时,选择决策点(j)比决策点(k)更优。而且由于(x[i])具有单调增的单调性,(-x[i])单调减,所以(i),(i+1),(i+2)…之后每一个点做决策时(j)都一定比(k)更优,所以我们可以直接把(k)省略掉,不再考虑。
Part 2
然后我们再来观察另外一个式子,
仍然是(k< j< i),我们考虑在什么情况下(j)这个决策点是无意义的。
设(a)、(b)两点连线的斜率为(s(a,b)),我们发现当(s(k,j)>s(j,i))时,设当前决策点为(t)。则如果(s(k,j) > -x[t]),则(k)比(j)更优;而当(s(k,j) < -x[t])时,(s(j,i) < s(k,j) < -x[t]),(j)比(k)更优,但同时(i)比(j)更优。所以无论如何,(j)永远不可能成为最优决策点,我们把它省略掉。
Part 3
然后我们便发现,如果我们用一个双端队列把这些可能会被用到的决策点依次存起来(按DP的顺序,也就是下标的从小到大或从大到小),根据我们上面所提到的,把不需要的决策点去掉,对留下来的点中任意相邻三个点(i、j、k),一定有(s(k,j) < s(j,i)),也就是说,这个斜率是单调增的(或者对于有些题是单调减)。正如以下这个图片:
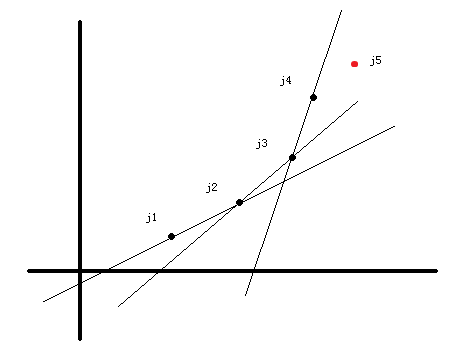
现在我们简单说一下如何维护这个单调队列,(j1)、(j2)、(j3)....是单调队列里当前正在维护的决策点,设我们的DP当前处理到了(i),也就是第(i)块土地。这些决策点还在单调队列里当且仅当这些点可能成为(i)、(i+1)、(i+2)...的最优决策点。
现在我们想要计算第(i)个点的(f[i]),首先我们要找出单调队列里哪个点是(i)的最优决策点,我们从队首开始看起,设队首的两个点为(j1)、(j2),我们计算( s(j1,j2) ),当( s(j1,j2) <= -x[t] )),(j2)比(j1)更优,我们把(j1)从单调队列中pop出来,以后也用不到了(见Part 1),然后再对( s(j2,j3) )进行比较;当( s(j1,j2) > -x[t] ),(j1)比(j2)更优,且因为队列的单调性(见Part 3),( s(j2,j3) > s(j1,j2) > -x[t] )),也就是说(j1)优于(j2)优于(j3)...,则(j1)是对于当前点(i)最优的一个决策。
然后有了决策点,我们就可以计算出(f[i])。现在我们来考虑将( (y[i+1],f[i]) )添加到单调队列中去。
假设我们要添加的点为(j5)(如上图中红点),设队尾的两个点为(j3)、(j4)。我们比较( s(j3,j4) )与( s(j4,j5) ),若( s(j3,j4) > s(j4,j5) ),则(j4)永远不可能是最优决策点(见Part 2),把(j4),也就是队尾的点弹出,再依次比较;若( s(j3,j4) < s(j4,j5) )满足斜率单调增的单调性,把(j5),也就是DP到的当前节点插入到队尾。
以上是对这个单调队列的理解,一句话总结,你需要维护一个存储决策点的队列,这个队列的相邻两个点的斜率单调。
注意
- 当队列里的点个数小于两个,你需要停止循环。
- 队列里一般会先放一个所有参数均为0((f[0])....)的点0作为哨兵,有可能有参数不为0(具体看题,反正我没有遇到过)。
代码

1 /* Stay hungry, stay foolish. */ 2 #include<bits/stdc++.h> 3 using namespace std; 4 template <class T> inline void read(T &x) { 5 int t; bool flag=false; 6 while((t=getchar())!='-'&&(t<'0'||t>'9')) ; 7 if(t=='-') flag=true,t=getchar(); x=t-'0'; 8 while((t=getchar())>='0'&&t<='9') x=x*10+t-'0'; 9 if(flag) x=-x; 10 } 11 const int maxn=50010; 12 struct Node { 13 long long x,y; 14 bool operator < (Node B)const { 15 if(x==B.x) return y<B.y; 16 return x<B.x; 17 } 18 }p[maxn]; 19 long long n,f[maxn],q[maxn]; 20 double slope(long long a,long long b) { 21 return (1.0*(f[a]-f[b]))/(p[a+1].y-p[b+1].y); 22 } 23 int main() { 24 //freopen("acquire.in","r",stdin); 25 //freopen("acquire.out","w",stdout); 26 read(n); 27 for(int i=1;i<=n;++i) read(p[i].x),read(p[i].y); 28 sort(p+1,p+n+1); 29 int cnt=0; 30 for(int i=1;i<=n;++i) { 31 if(p[i].y<=p[i+1].y) continue; 32 while(cnt&&p[cnt].y<=p[i].y) --cnt; 33 p[++cnt]=p[i]; 34 } 35 //读入并将多余的土地删除 36 int h=0,t=1; 37 q[h]=0; //设置哨兵 38 for(int i=1;i<=cnt;++i) { 39 while(t-h>1&&slope(q[h],q[h+1])>=-p[i].x) ++h; //删除队首非最优决策点 40 f[i]=f[q[h]]+p[q[h]+1].y*p[i].x; //计算当前点DP值 41 while(t-h>1&&slope(q[t-2],q[t-1])<slope(q[t-1],i)) --t; //删除队尾非最优决策点 42 q[t++]=i; //把当前点插入队尾 43 } 44 cout<<f[cnt]<<endl; 45 return 0; 46 }
题目推荐
以下推荐几道看了本文可以去水掉的题:
