Description
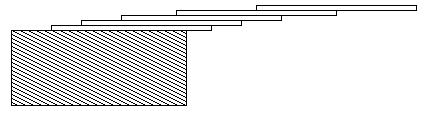
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
Input
Output
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
Source
根据题意可建立以下数学模型: 令 ∑(1/n) >= c 其中 n∈[2, ∞), c∈[0.01, 5.20]且其精度含小数在内最多3个数字 给定c 求 n (若c在范围外,则不求解) 分析: 本质就是变种的调和数列求和(数列中缺少1) 但调和数列是发散的,不存在准确的求和公式,只有近似公式: 调和数列 ∑(1/n) ~ ln(n+1) + R 其中 n∈[1, ∞), R为欧拉常数(R = 0.5772156649...) 但近似公式只有在n非常大的时候误差才可以忽略不计, 当n很小时,对本题而言误差是不可接受的。 因此本题用常规解法即可 (由于前n项和是固定的,用打表法也可, 不过题目考核范围较小,打表意义也不大)
#include <iostream> using namespace std; /* * 根据调和数列的和值反求项数 * @param sum 目标和值 * return 调和数列项数 */ int harmonicSeries(double sum); int main(void) { double sum = 0.0; while(true) { cin >> sum; if(sum < 0.01 || sum > 5.20) { break; } int n = harmonicSeries(sum); cout << n << " card(s)" << endl; } return 0; } int harmonicSeries(double sum) { int n = 2; double curSum = 0.0; while(curSum < sum) { curSum += (1.0 / n++); } return n - 2; // n从2开始因此项数-1, 最后一次求和多了一次n++也要-1, 因此共-2 }