所谓边缘就是指图像局部亮度变化最显著的部分,它是检测图像局部变化显著变化的最基本的运算。对于数字图像,图像灰度灰度值的显著变化可以用梯度来表示,以边缘检测Sobel算子为例来讲述数字图像处理中边缘检测的实现:
对于数字图像,可以用一阶差分代替一阶微分;
△xf(x,y)=f(x,y)-f(x-1,y);
△yf(x,y)=f(x,y)-f(x,y-1)
求梯度时对于平方和运算及开方运算,可以用两个分量的绝对值之和表示,即:
G[f(x,y)]={[△xf(x,y)] +[△yf(x,y)] } |△xf(x,y)|+|△yf(x,y)|;
Sobel梯度算子是先做成加权平均,再微分,然后求梯度,即:
△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);
△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);
G[f(x,y)]=|△xf(x,y)|+|△yf(x,y)|;
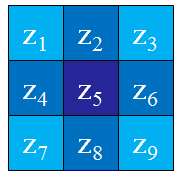
上述各式中的像素之间的关系见图
| f(x-1,y-1) | f(x,y-1) | f(x+1,y-1) |
| f(x-1,y) | f(x,y) | f(x+1,y) |
| f(x-1,y+1) | f(x,y+1) | f(x+1,y+1) |
边缘
边缘(edge)是指图像局部强度变化最显著的部分。主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间,是图像分割、纹理特征和形状特征等图像分析的重要基础。
图像强度的显著变化可分为:
- 阶跃变化函数,即图像强度在不连续处的两边的像素灰度值有着显著的差异;
- 线条(屋顶)变化函数,即图像强度突然从一个值变化到另一个值,保持一较小行程后又回到原来的值。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈.边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。

(a)(b)分别是阶跃函数和屋顶函数的二维图像;(c)(d)是阶跃和屋顶函数的函数图象;(e)(f)对应一阶倒数;(g)(h)是二阶倒数。
一阶导数法:梯度算子
对于左图,左侧的边是正的(由暗到亮),右侧的边是负的(由亮到暗)。对于右图,结论相反。常数部分为零。用来检测边是否存在。
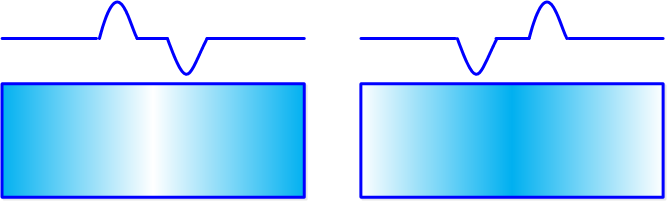
梯度算子 Gradient operators
函数f(x,y)在(x,y)处的梯度为一个向量:
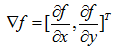
计算这个向量的大小为:
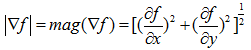
近似为:
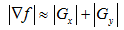
梯度的方向角为:
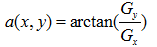
Sobel算子
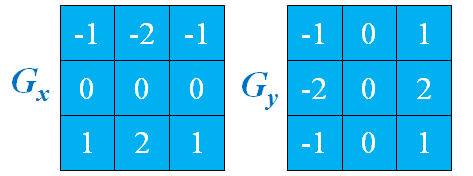
sobel算子的表示:

梯度幅值:
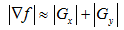
用卷积模板来实现:
【相关代码】
接口
使用
二阶微分法:拉普拉斯
二阶微分在亮的一边是负的,在暗的一边是正的。常数部分为零。可以用来确定边的准确位置,以及像素在亮的一侧还是暗的一侧。

LapLace 拉普拉斯算子
二维函数f(x,y)的拉普拉斯是一个二阶的微分,定义为:
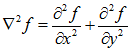
其中:
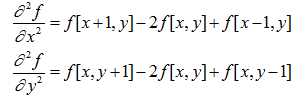
可以用多种方式将其表示为数字形式。对于一个3*3的区域,经验上被推荐最多的形式是:

定义数字形式的拉普拉斯要求系数之和必为0
【相关代码】
接口
使用
实践效果
原图

注意,边缘检测对噪声比较敏感,需要先用高斯滤波器对图像进行平滑。参考博文:【OpenCV】邻域滤波:方框、高斯、中值、双边滤波
Sobel 边缘检测

Sobel算子可以直接计算Gx 、Gy可以检测到边的存在,以及从暗到亮,从亮到暗的变化。仅计算| Gx |,产生最强的响应是正交 于x轴的边; | Gy |则是正交于y轴的边。
Laplace边缘检测
拉普拉斯对噪声敏感,会产生双边效果。不能检测出边的方向。通常不直接用于边的检测,只起辅助的角色,检测一个像素是在边的亮的一边还是暗的一边利用零跨越,确定边的位置。
转载请注明出处:http://blog.csdn.net/xiaowei_cqu/article/details/7829481
实验代码下载:http://download.csdn.net/detail/xiaowei_cqu/4475976
