2019牛客暑期多校训练营（第三场）D Big Integer

题目链接

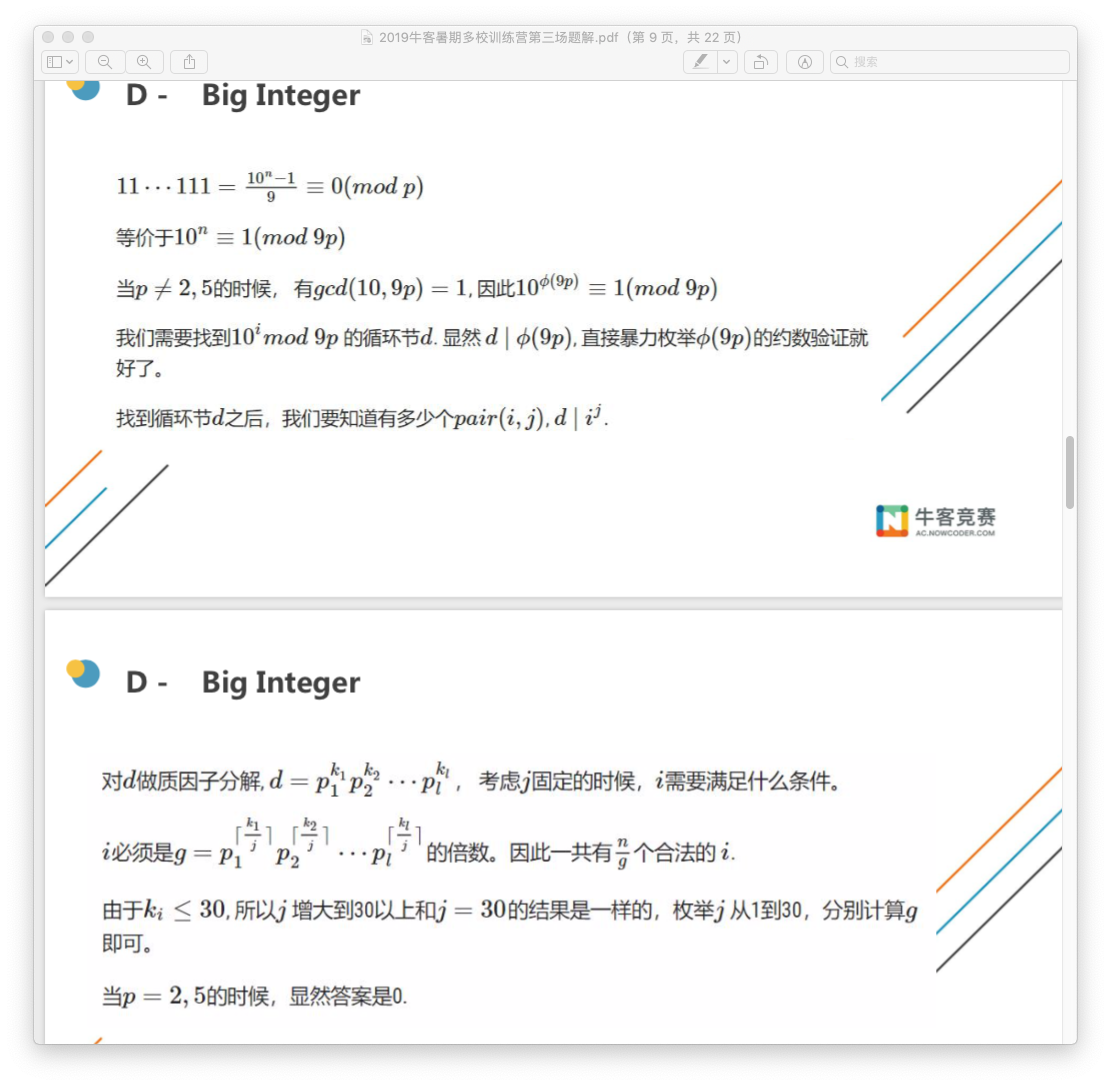
比赛的时候找到d之后就卡住了，不知道怎么找(i^j)中有多少个d的倍数，没有想到可以先固定j，然后看对于当前j有多少个i

快速幂的时候long long 溢出了……

#include "bits/stdc++.h"

using namespace std;
typedef long long ll;
ll mod;

ll powmod(ll a, ll b) {
    ll ret = 1;
    while (b) {
        if (b & 1) ret = (__int128) ret * a % mod;
        a = (__int128) a * a % mod;
        b >>= 1;
    }
    return (ll) ret;
}

struct node {
    ll p, cnt;
} prime[50];
int tot = 0;

ll phi(ll n) {
    tot = 0;
    ll ans = n;
    int to = sqrt(n);
    for (ll i = 2; i <= to; i++) {
        if (n % i) continue;
        prime[++tot].p = i;
        prime[tot].cnt = 0;
        ans = ans / i * (i - 1);
        while (n % i == 0) {
            prime[tot].cnt++;
            n /= i;
        }
    }
    if (n > 1) {
        ans = ans / n * (n - 1);
        prime[++tot].p = n;
        prime[tot].cnt = 1;
    }
    return ans;
}


int getx(ll euler, ll p) {
    ll ret = 1e18;
    for (ll i = 1; i * i <= euler; i++) {
        if (euler % i) continue;
        if (powmod(10, i) == 1) ret = min(ret, i);
        if (powmod(10, euler / i) == 1) ret = min(ret, euler / i);
    }
    return ret;
}

int main() {
//    freopen("in.txt", "r", stdin);
    int _;
    ll p, n, m;
    scanf("%d", &_);
    while (_--) {
        scanf("%lld %lld %lld", &p, &n, &m);
        if (p == 2 || p == 5) {
            printf("0
");
            continue;
        }
        mod = 9 * p;
        ll euler = phi(9 * p);
        ll x = getx(euler, p);
        phi(x);
        ll ans = 0;
        ll te;
        for (int j = 1; j <= 30; j++) {
            if (j > m) break;
            te = 1;
            for (int i = 1; i <= tot; i++) {
                ll t = (prime[i].cnt + j - 1) / j;
                te = te * pow(prime[i].p, t);
            }
            ans += n / te;
        }
        if (m > 30) {
            ans += n / te * (m - 30);
        }
        printf("%lld
", ans);
    }
    return 0;
}