matlab学习笔记之五种常见的图形绘制功能

分类：

• 离散数据图形绘制
• 函数图形绘制
• 网格图形绘制
• 曲面图形绘制
• 特殊图形绘制

本文重点介绍matlab五种图形绘制方法的后三种。

一、网格图形绘制

以绘制函数z=f(x,y)三维网格图为例，下面为绘制步骤：

1. 确定自变量x和y的取值范围和取值间隔

　　　　x = x1:dx:x2; y = y1:dy:y2;

　　2.构成xoy平面上的自变量采样格点矩阵

　　　　1）  利用“格点”矩阵生成原理生成矩阵

　　　　　　X = ones(size(y))*x; Y = y*ones(size(x));

　　　　2）  利用meshgrid命令生成“格点”矩阵

　　　　　　[X,Y] = meshgrid(x,y);

　　3.计算在自变量采样“格点”上的函数值

　　　　1）  mesh(X,Y,X)

　　　　2）  mesh(Z)

　　　　3）  mesh(X,Y,Z,C)

　　　　4）  mesh(X,Y,Z,’PropertyName’,PropertyValue,...)

实例：绘制的图像，并作定义域的裁剪。

clear,clf,

a = -1;b = 1;c = -15;d = 15;n = 20;eps1 = 0.01;

x = linspace(a,b,n);y = linspace(c,d,n);

[X,Y] = meshgrid(x,y);

% 计算函数值z，并做函数的定义域剪裁

for i = 1:n

    for j = 1:n

        if(1-X(i,j))<eps1 || X(i,j) - Y(i,j) < eps1

            Z(i,j) = NaN;

        else

            Z(i,j) = 1000*sqrt(1 - X(i,j))^-1.*log(X(i,j)-Y(i,j));

        end

    end

end

% 画定义域边界线

zz = -20*ones(1,n);plot3(x,x,zz),grid on,hold on

mesh(X,Y,Z)

view([-56.5 38]);

xlabel('x'),ylabel('y'),zlabel('z'),box on

结果：

 

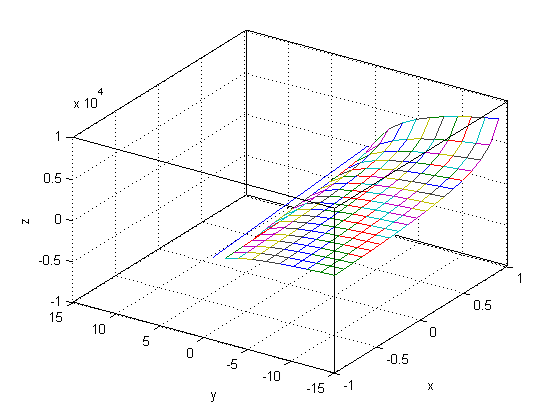
二、曲面图形绘制

曲面图形的绘制使用surf函数完成，与mesh函数类似。

surf函数使用方式：

　　1）surf(X,Y,X)

　　2）surf(Z)

　　3）surf(X,Y,Z,C)

　　4）surf(X,Y,Z,’PropertyName’,PropertyValue,...)

实例：绘制圆锥体曲面。

clc,clear,close all

X = -10:1:10;

Y = -10:1:10;

[X,Y] = meshgrid(X,Y);

Z = sqrt(X.^2 + Y.^2);

surf(X,Y,Z)

xlabel('x')

ylabel('y')

zlabel('z')

box on

axis tight

colormap(lines)

shading interp

set(gca,'Ydir','reverse');

set(gcf,'color','w');

结果：

 

 三、特殊图形绘制

Matlab对于不同的三维曲面的绘制提供了不同的画图函数，如slice切片函数、quiver3三维箭头标记函数、sphere等。下面以绘制空间曲线及其运动为例抛砖引玉：

已知空间曲线的方程为：

%   空间曲线的绘制

clc,clear,close all

t = 00:0.1:1.5;     % 设置运动时间

% 给定曲线方程

x = t.^2;

y = (2/3)*t.^3;

z = (6/4)*t.^4-(1/3)*t.^3;

plot3(x,y,x,'r.-'),hold on,grid on

% 计算各方向梯度

Vx = gradient(x);

Vy = gradient(y);

Vz = gradient(z);

% 绘制速度矢量图

quiver3(x,y,z,Vx,Vy,Vz);

xlabel('x')

ylabel('y')

zlabel('z')

结果：

 

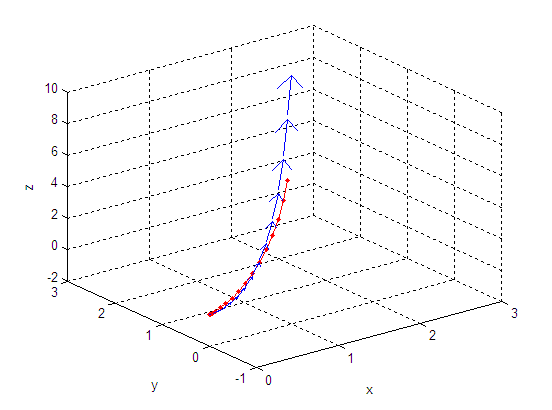
 欢迎探讨。