看完这篇就懂了。
IoU
intersect over union,中文:交并比。指目标预测框和真实框的交集和并集的比例。
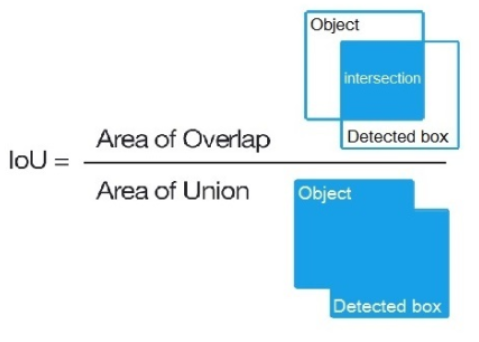
mAP
mean average precision。是指每个类别的平均查准率的算术平均值。即先求出每个类别的平均查准率(AP),然后求这些类别的AP的算术平均值。其具体的计算方法有很多种,这里只介绍PASCAL VOC竞赛(voc2010之前)中采用的mAP计算方法,该方法也是yolov3模型采用的评估方法,yolov3项目中如此解释mAP,暂时看不明白可以先跳过,最后再回过头来看就能明白了。

比如我们现在要在一个给定的测试样本集中计算猫这个类别的AP,过程如下:
首先,AP要能概括P-R曲线的形状,其被定义为采用如下公式来计算:
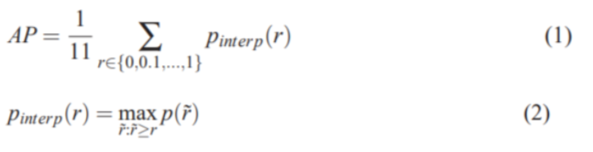
那么,我们先来看看P-R曲线是什么:用蓝色笔迹遮住的部分不需要关注。
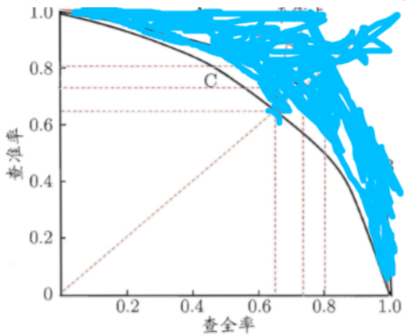
图中的曲线C就是一条P-R曲线,P表示纵轴的查准率precision,R表示横轴的召回率或称为查全率recall。P-R曲线下的面积可以用于评估该曲线对应的模型的能力,也就是说比较2个目标检测模型哪个更好,可以用P-R曲线面积来比较,面积越大模型越好。然而可能是因为这个面积并不好计算,所以定义了公式(1)来计算出一个叫AP的东西,反正这个东西也能体现出precision和recall对模型能力的综合影响。
从公式(2)可以知晓,Pinterpo(r)表示所有大于指定召回率r的召回率rhat所对应的的p的最大值。大于某个r的rhat有很多,我们要找到这些rhat中所对应的p是最大的那个,然后返回这个p。公式(1)中规定了r会从0-1.0以0.1为步长取11个值,然后将这11个r对应的11个p累加求算术平均值就得到了AP。所以我们要先得到一组rhat和p,这需要我们先了解recall和precision是如何计算的。
我们先来看看P(precision)和R(recall)的计算公式:
precision = TP / (TP+FP)
recall = TP / (TP+FN)
TP是检测对了的正样本,FP是检测错了的正样本,FN是漏检的正样本。
对于目标检测模型一般最后都会输出一个置信度(如果样本图片中有不止一个目标,本例中只选择猫类别的置信度即可),所以可以设置一个置信度阈值,比如0.6,那么高于0.6的就认为该样本被检测为了正样本(即检测为猫),这样我们会得到0.6阈值下的一组正样本。
然后在这组正样本的基础上,设定一个IoU的阈值,其值为0.5(意思是检测为猫的目标的预测边界框和真实边界框的交并比要大于0.5),大于该阈值的认为是TP,其它的认为是FP。然后用测试样本中真实的正样本数量减去TP,就得到了FN。
这样,在置信度阈值为0.6的情况下,我们就得到了一对P(precision)和R(recall),接着我们取不同的置信度阈值,得到更多的P-R对,然后根据公式(2)找到所有大于指定召回率r的召回率rhat所对应的的p的最大值(采用这种方法是为了保证P-R曲线是单调递减的,避免摇摆),作为当前指定召回率r条件下的最大查准率p,然后根据公式(1)计算出AP。这个AP就是猫这个类别的AP,接着我们可以计算其它类别的AP,然后对这些AP求算术平均值,就得到了mAP。
了解了mAP之后,我们就容易理解为什么目标检测模型的度量指标不能像图像分类模型那样直接计算一遍precision和recall,因为目标检测任务中会包含多个类别的目标,并且除了给目标分类,还要预测目标的边界框,所以要加入IoU的概念,并考虑多个类别,而mAP就是在考虑了IoU和多类别之后计算出的度量指标。
参考文献:
http://homepages.inf.ed.ac.uk/ckiw/postscript/ijcv_voc09.pdf
https://github.com/AlexeyAB/darknet