Description
Solution
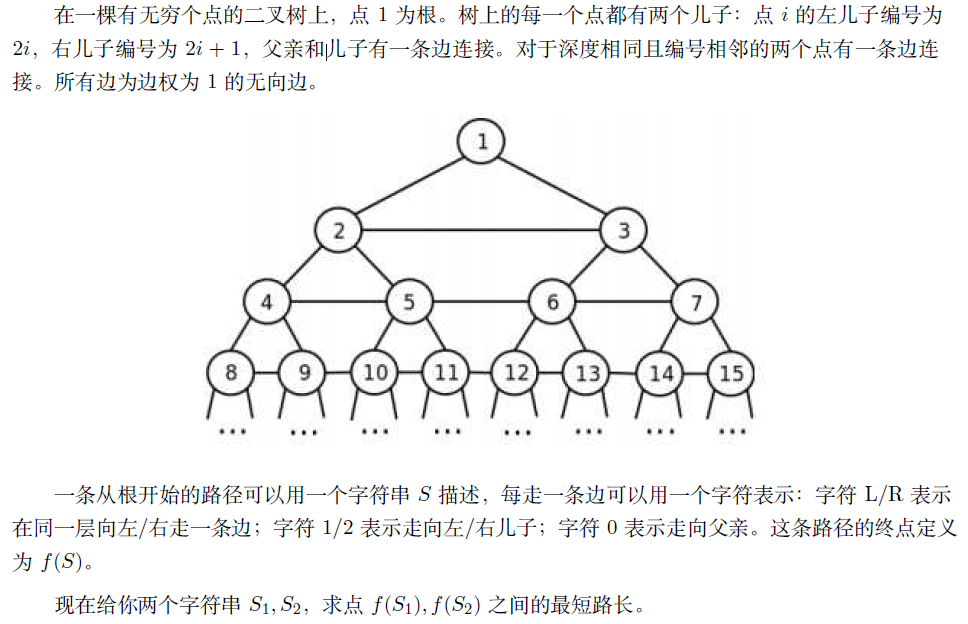
首先根据手动模拟,可以发现对于两个节点(A,B),首先必须要花费一些代价向上跳到同一深度。
然后再让(A,B)同时向上跳,中途可能(A,B)再通过只走横向的边相遇。这样就可以维护最小值,求出答案了。
现在主要的问题就是要怎么写高精度。注意到我们需要维护一个初始值为(1)的数(x),并支持以下(3)种操作:
(1.)乘以(2)(并加上(1));
(2.)除以(2)并下取整;
(3.)加减(1)。
所以可以用二进制高精,并将输入操作序列转化为只有向下移动的序列,这样就方便操作了。
我们维护一个数组 (a_{1}, cdots, a_{n},) 表示当前数为 (sum_{i=1}^{n} a_{i} 2^{n-i})。((0)是向左,(1)是向右)加减(1)的操作直接做,乘以(2)(并加上(1))的操作就把(n)加上(1),并让(a_n=0/1),除以(2)的就先维护进/退位,再把(n)减(1)即可。处理完后,再从后往前维护一遍进/退位。
(处理进/退位:a[pos - 1] += ((a[pos] - (a[pos] & 1)) >> 1); a[pos] &= 1;)
但是这样做为什么是对的呢?
注意到对(a)序列进行的操作,都唯一且恰好对应对数(x)(即当前节点编号)的操作。且因为我们维护了进位,所以通过(a)序列算出来的数值一定和(x)相等。从而这样是可以做的。
于是先把输入的操作序列转化为两个序列(a,b),再维护一个(Delta)表示(A,B)(在同一层)的横向距离,手模可以发现(Delta = 2 * Delta + a[i] - b[i])。再通过之前说的方法,既可以求出答案。
当然,如果计算过程中(Delta)的值过大,可以直接(break)掉(这时肯定不会是答案)。
时间复杂度(O(n+|S|))。