笔者本着破除大多数新手对于算法恐惧的目的,加深对算法的了解,通过介绍一系列算法解法的产生过程,培养算法求解能力。为便于新手学习,本文不会有严谨、复杂的数学推导。
面向对象:期望对算法产生过程有透彻了解的同学;注意,本文介绍的算法求解思路过程对于算法高手来说过于繁琐,但说不定也能引起高手们问题求解时灵光一闪的回忆。
目标:期望各位同学能够自如的面对非算法岗的算法和编程面试题目。
下面进入正题,看看下面两个链表问题(算是链表面试题目中有点难度的问题)。
①如何判断一个链表有环?
②基于问题①,如何找到该环的起始位置?以下图为例,也就是找到节点4。
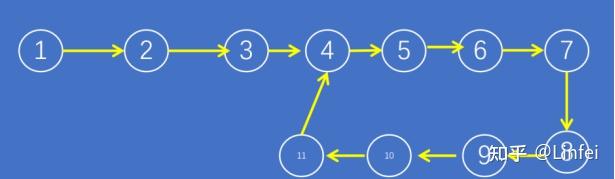
图1-链表示例(注:本图是从笔者在知乎的专栏拷贝过来)
注意:解决本题目,需要具备链表的基础知识(新建、遍历,链表的概念),大家可以自行从网上查阅。
对于问题①,聪明的同学或者刷过题目的同学很容易得到答案。
万一你是算法初学者,经验欠缺,怎么解这道题呢?
我们知道,解题时,首先要知道和题目相关的知识点:
先看看教材中学到的链表常规操作有哪些?
1)新增节点
2)删除节点
3)遍历
4)修改内容
基于已有的知识点,下面我们开始分析:
1)操作1、2、4表面上看起来和本问题无关,故而先放一边。
2)先考虑动作3,也就是遍历(遍历很容易理解,就是挨个访问链表的每个节点)。
那么,是否可以基于遍历来判断链表有环呢?我们开始尝试。
首先认清这样一个事实,如果只是挨个访问节点,没有其他辅助手段的话,是没办法得到答案的。
如果大家学过算法课的话,有个问题求解的基本方法:就是空间换时间。
在本问题里,可以通过利用额外的空间来解决问题。思路如下:
挨个遍历,能够得到每个节点的地址,保存这些访问过的旧节点地址。每次访问下一个新节点时,判断新节点是否在之前出现过,如果出现过,说明有环。
具体写程序时,用一个数组(高级一点的话,hashmap也行)来记录访问过的地址,每次访问到新节点时,将新节点的地址和数组里的地址逐一进行比较,如果和某个地址相等,则认为有环。
此时,我们得到了第一个解法。本解法的优点是思路比较清晰,容易理解;存在的问题是链表很长的话,时间复杂度可以是 )或者O(N)的(取决于用数组保存还是hashmap保存已经访问过的节点);同时,使用的额外存储空间也是O(N),当N比较大时,需要占用较多的内存。
有没有更好的解法呢?大多数情况不存在上帝视角,我们不知道是否有更好的解法。解决办法:一是去问大拿,二是自行探索,提升问题解决能力,最起码可以加深对此类题目的印象。
说起自行探索,问题探索能力取决于大家各自的知识沉淀。基本做法如下:
依赖于自身的知识,按照问题解决的各种思路,逐一进行试验。
据说解决问题的次数多了以后,面对全新问题会形成一种直觉,下意识的知道用什么办法来解决,笔者还没达到这种境界,大家一起努力吧。
下面尝试一种方法:也就是基于自身的学习和生活经验,找类似现象或问题。
这个问题和我们遇到的哪些问题或者现象类似呢? 本题目的特征是环。提到环,联想到大家上大学时,体育场通常都有环形跑道,环形跑道有个特点,就是你在跑步时,如果速度够快的话(大家想想美国队长2开头队长和猎鹰跑步的场景),肯定能超过速度慢的人,大家跑的圈数多的话,可以多次超过。
整理一下思路,此时的关键点: 在环形跑道上,你能够追上速度比你慢的人。
进一步推断: 在一个跑道上, 运动员A和B同时起跑,A比B的速度快,后面A还能追上B的话,说明该跑道一定是环形跑道。
类比到链表:
A和B可以对应两个指针slow和fast,后面简称为s和f。
速度快慢对应指针每次移动的次数。
那么,如何设定2个指针每次移动的次数呢?只需要设定f每次比s的速度多移动1个节点即可。具体来说,可以设定s每次移动1个节点,f每次移动2个节点(大家可以思考下,f如果每次比s多移动2个节点或以上时,会出现什么情况?)
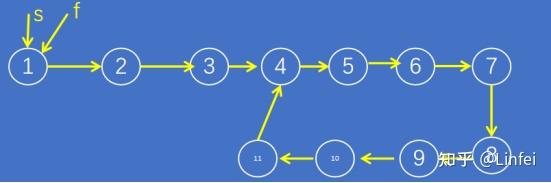
图2-使用两个指针s,f指向链表头部
通过简单的数学运算,发现最终在节点9,f追上s。 算法代码代码如下:
class node:
def __init__(self,val,next=None):
self.val = val
self.next = next
def is_linklist_cyclic(link_list):
if not link_list:
return False
s = link_list
f = link_list
while True:
f = f.next
if not f:
return False
f = f.next
if not f:
return False
s = s.next
if f == s:
return True
#构造例子中的循环链表
def create_link_list():
head_node = node(11)
tail_node = head_node
cyclic_head_node = None
for i in range(1,11):
tmp_node = node(11-i,head_node)
head_node = tmp_node
if 11-i == 4:
cyclic_head_node = tmp_node
tail_node.next = cyclic_head_node #11号节点链接到4号节点,构建环
return head_node
def test_is_link_cyclic():
#构造例子中的循环链表
head_node = create_link_list()
print(is_linklist_cyclic(head_node))
test_is_link_cyclic()很幸运,我们初次尝试就找到了答案,实际问题求解过程中,可能要尝试多种方法才能找到最终解答。
下面再看第二个问题,如何找到环的起始位置,也就是上图中的节点4。
此时我们没有明确的思路,还是先对题目探索一下,看看能不能找到解决办法。
此时思路可能比较混乱。没关系,运气好的话,你可能会先看看当f追上s时,f的位置在哪儿?
假设从链表头节点到环的起始点C的长度是L(以例子里的链表为例,L=3), 环的长度是N(例子里的链表中,环的长度为8)。
要注意的是,C、L、N目前都是未知数,只是为了便于分析,我们赋予了它们含义。
那么,当s到达节点C时,共移动了L步,此时s一共移动了2*L步,也就是如下情况:
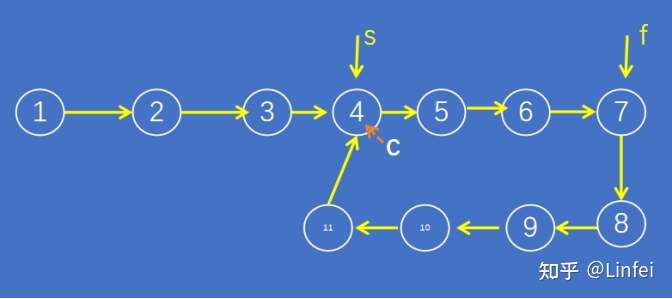
图3-s到达环起始节点C时,f在C后面L步的节点
很容易看出,此时s落后f的步数为L,同时,双方已经在一个环形内部了。
此时此刻,f距离s为N-L步(本例中f距离s为5步)。
基于s每次移动1步的事实,当s移动N-L步时,f移动了2(N-L)步,此时,f追上了s。也意味着在环内部距离起始位置C的距离为N-L的地方,f追上了s。如下图所示:
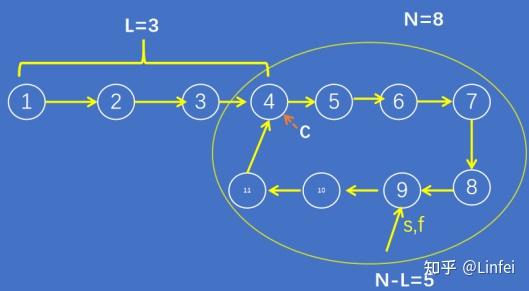
图4:s和f还差N-L步就可以到C
下一步怎么办?
大家观察一下,此时s和f距离环的起始点C的距离是N-(N-L)=L,这个事实大家可以注意一下,也就是说此时s和f距离起始点C的距离和链表头部节点(上例中为1所在的节点)到C点的距离相等,都是L。
此时情形可以想象一下,两个人A和B,A在链表头节点1处,B在s处,二者距离C都是L步,此时我们要求的就是C。
答案大家能想出来了吧?我们安排A和B同时以相同的速度出发,就一定会在点C处相遇。对应到链表,就是把s重置到链表头节点,速度为每次一个节点,f的速度也调整为每次一个节点,二者同时出发,当f和s相等时,即达到了C点,也就是找到了环的头节点。
下面是示例代码。
class node:
def __init__(self,val,next=None):
self.val = val
self.next = next
def find_cyclic_head(link_list):
if not link_list:
return False
s = link_list
f = link_list
while True:
s = s.next
if not s:
return False
f = f.next
if not f:
return False
f = f.next
if not f:
return False
if s == f: #第一次相遇
break
s = link_list #重设s到链表头节点
while not (s==f):
s = s.next
f = f.next
return s
def test_get_cyclic_head():
link_list = create_link_list()
cyclic_head = find_cyclic_head(link_list)
print("环首节点值:",cyclic_head.val)
test_get_cyclic_head()
这种办法的时间复杂度为O(N),额外的空间复杂度为O(1),会比第一种算法更优秀一些。
再思考一下,问题解决了么?
上图中,我们还有个隐藏假设,就是环的长度N大于L,如果环的长度小于L时会发生什么呢?好消息是上面的代码不用做任何改动,同样适合本情形,但具体发生了什么就不一样了。下面来分析一下,我们把链表做了一下调整:
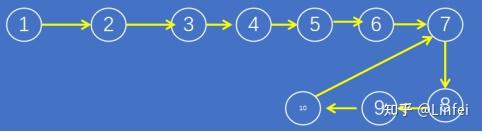
图5- 带环链表
这里L=6,N=4。
首先还是分析当s到达节点C时,f在哪个位置。结合前面的分析,此时f已经在环中移动了L,但由于L>N,f至少已经重新遍历了环的起始节点C一次,精确来说,f距离C为(N-L%N),s距离f为L%N。
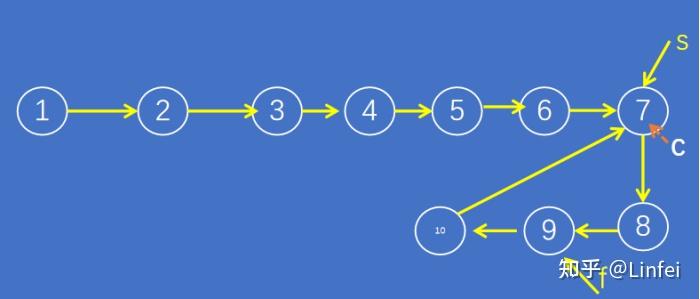
图6-s到达C时,f的位置
同之前的分析,f追上s时,s在距离C点N-L%N的位置,也就是图中的9号节点。
此时,f和s距离C为N-(N-L%N) = L % N。
现在,整理一下思路,目前有以下事实:
1)链表起始位置到C的距离是L
2)f距离C的距离是 L%N
下一步怎么办?先看看L、L%N和N的关系。
按中学的知识,数字之间的关系通常能想到的是整除。分析得到 L - L %N 肯定是可以被N整除的。
接着探索,借鉴前面的经验,假设s和f重新设置为分别从链表头部节点1和节点9出发,速度都是每次前移1个节点。则当f到达环的起始节点C(也就是图例的节点7)时,s到达节点3。
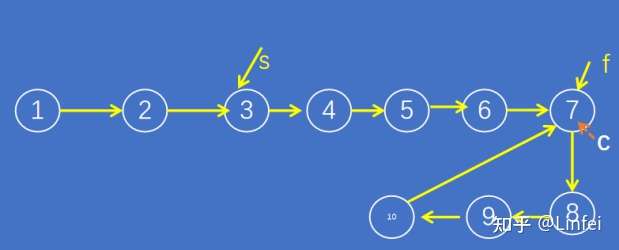
图7-s到达3时,f到达环的起始节点C
抽象来看,s距离点C还有 L - L%N的距离,f在点C。 又基于前面提到的(L-L%N)是N的倍数(例如上面例子中,L-L%N=4,N=4,L-L%N正好是N的1倍),可以知道当s从节点3走了L-L%N步到达C时,f同样从C点出发走了L-L%N步,又L-L%N是N的倍数,就是说f肯定还在点C(f走的圈数是L/N)。此时s=f,问题得以解决。
从代码角度来说,不需要做任何修改。第一步得到s和f相等的位置,第二步设置s到起始点,第三步f和s以相同的速度(每次前移一个节点)运行,直到二者相等。
小结:
1)做题时有信心,基于少量的知识点(本例中的整除),也是有可能解决问题的。哪怕不一定能找到答案,也是对你逻辑思维能力很好的锻炼。
2)遇到不明白的问题,多探索,具象化问题,加深对问题的了解。
3)没解决思路时,可以尝试联想平时生活中遇到的类似问题或现象,找灵感
4)定时整理思路和已有的条件,看看是否有新的解题突破