1.
设F是由T1、T2和T3三棵树组成的森林,与F对应的二叉树为B,T1、T2和T3的结点数分别为N1、N2和N3,则二叉树B的根结点的左子树的结点数为 N1-1 。
由森林转化为二叉树的规则可知,T2、T3是转化为T1的右子树的,T1去掉一个根节点,所以二叉树B根节点的左子树节点数为N1-1。
2.
设完全二叉树的第6层有24个叶子结点,则此树最多有 79 个结点。
根据完全二叉树每层结点总数最大值的计算公式可以算出第6层最多有26-1=25=32个结点。其中有24个叶子结点,假设他们全部在该层靠右排列,那么在这一层还有32-24=8个非叶子结点,由此可以推断第7层还有2×8=16个叶子结点,因为上一层靠左的8个结点都有两个孩子。综上所述,该完全二叉树最多有1+2+4+8+16+32+16=79个结点。
3.
已知一棵二叉树的前序遍历结果为 ABCDEF,中序遍历结果为 CBAEDF,则后序遍历的结果为 CBEFDA 。
4.
F 是一个森林,B 是由 F 变换得的二叉树。若 F 中有 n 个非终端结点,则 B 中右指针域为空的结点有 n+1 个。
树变成二叉树的情况:
(1)根节点无右兄弟,右指针域一定为空; -----------------1个
(2)除根节点之外的每个非终端节点都有孩子,其下的分支一定有最终的叶子节点,右指针域为空;-----------------n-1个
(3)其中最后一个非终端节点无右兄弟,右指针域也为空。-------------------加1个
(4)因此,共有n+1个。
而若是森林的话:
(1)首先是每个树转变为相应的二叉树,再合成一棵二叉树:
(2)假设m棵树,每棵树变成二叉树右指针域为空的节点数均加一,则一共加了m;
(3)而二叉树连成树的过程中,前m-1个树的根节点变化过程中都有了右孩子(最后一个右指针域仍为空),因此要减去m-1;
(4)故符合要求的节点数一共为:n+m-(m-1)=n+1 n为n1+n2+n3+...+nm,森林中每棵树的非终端结点树之和
5.设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为7、19、2、6、32、3、21、10,根据这些频率作为权值构造哈夫曼树,则这棵哈夫曼树的高度为 6 。
构造出这棵哈夫曼树。
6.
设G是一个非连通无向图,有15条边,则该图至少有 7 个顶点。
根据连通图的性质以及顶点与边数的关系即可求解:设无向图有n个顶点,它的边数e<=n(n-1)/2。若e=15,则可求解得n>=6。在连通图情形下至少需有6个顶点,在非连通图情形下则至少需有7个顶点。
7.
设某棵完全二叉树中有130个结点,则该二叉树中有个叶子结点 65 。
n0=n2+1
n2=n0-1
n=n0+n1+n0-1
n=2n0+n1-1
因为是完全二叉树,所以度为1的结点只能有1个或者0个,这里n1=1个,度为0的结点才有整数个。
所以:130=2n0+1-1 所以有n0=65
8.
设有向无环图G中的有向边集合E={<1,2>,<2,3>,<3,4>,<1,4>},则下列属于该有向图G的一种拓扑排序序列的是( A )。
(A) 1,2,3,4 (B) 2,3,4,1 (C) 1,4,2,3 (D) 1,2,4,3
9.
如下有向带权图,若采用迪杰斯特拉算法求源点a到其他各顶点的最短路径,得到的第1条最短路径的目标顶点是b,第2条最短路径的目标顶点是C,后续得到的其余各最短路径的目标顶点依次是 C 。
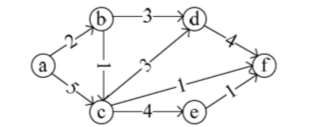
(A) d,e,f (B)e,d,f (C) f,d,e (D) f,e,d
10.
求下面带权图的最小(代价)生成树时,可能是克鲁斯卡尔(kruskal)算法第2次选中但不是普利姆(Prim)算法(从V4开始)第2次选中的边是( C )

A.(V1,V3) B(V1,V4) C(V2,V3) D(V3,V4)
从V4开始,Kruskal算法选中的第一条边一定是权值最小的(V1,V4),B错误。由于V1和V4已经可达,第二条边含有V1和V4的权值为8的一定符合Prim算法,排除A、D。
11. 设有数据逻辑结构为: B=(K,R) K={k1,k2,…,k9} R={<k1,k3>,<k1,k8>,<k2,k3>,<k2,k4>,<k2,k5>,<k3,k9>,<k5,k6>,<k8,k9>,<k9,k7>,<k4, k7>,<k4,k6>} 画出这个逻辑结构的图示,并确定相对于关系R,哪些结点是开始结点,哪些结点是终端结点?
该题的逻辑结构图示如图下所示。 开始结点是指无前趋的结点这里满足该定义的开始结点为k1k2。 终端结点是指无后续的结点这里满足该定义的终端结点为k6k7。 该逻辑结构是非线性结构中的图形结构。
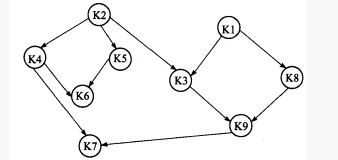
该题的开始结点是指无前趋的结点,这里满足该定义的开始结点为k1,k2。终端结点是指无后续的结点,这里满足该定义的终端结点为k6,k7。该逻辑结构是非线性结构中的图形结构。
12.
画出下图AOE网的关键路径
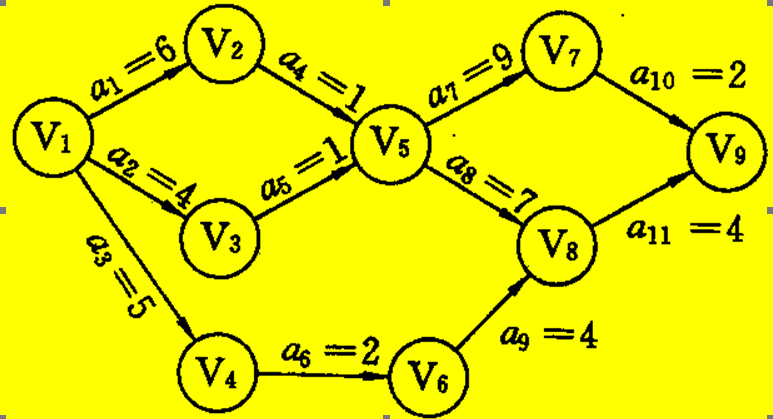
第一条关键路径a1a4a7a10、第二条关键路径a1a4a8a11

13. 编程题:设计计算二叉树中所有结点值之和的算法。
先序遍历二叉树的变形。
int Sum(BiTree * bt,int & count) { if(bt==NULL) { return 0; }else{ count+=bt->data; Sum(bt->lchild,count); Sum(bt->rchild,count); } }
14. 编程题:将一个无向图的邻接矩阵A转换为邻接表B。
设置一个空的邻接表,填入对应的顶点信息,然后在邻接矩阵上查找非零元素,找到后在邻接表对应边表中插入相应的边表结点。
//A是邻接矩阵,B是邻接表 void MatToList(MGraph A,ALGraph & B) { //vertex是顶点数,arcNum是边数 B.vertexNum=A.vertexNum; B.arcNum=A.arcNum; //写入邻接表 for(i=0;i<A.vertexNum;i++) { B.adjlist[i].vertex=A.vertex[i]; B.adjlist[i].firstedge=NULL; } //写入边表 for(i=0;i<A.vertexNum;i++) { for(j=0;j<A.vertexNum;j++) { //若在邻接矩阵中顶点i到顶点j之间存在边,在邻接表对应边表中插入相应的边表结点 if(A.arc[i][j]!=0) { ArcNode *p=new ArcNode; p->adjvex=j; //摘链操作 p->next=B.adjlist[i].firstedge; B.adjlist[i].firstedge=p; } } } }