题目链接 http://codeforces.com/problemset/problem/1292/A
大意
有一个(2×n)的迷宫,每次可以让一个块不能通过,问每次修改后是否可以从起点到终点/
分析1
先说说我的想法,暴力的话(O(NM)),时限是(1.5s),好像是差不多,但是一般卡着时间效率的代码都会T掉,所以暴力肯定不行,因为只有0和1俩状态,可以用(bitset)但我(bitset)只会用(count),所以还是算了。再想的话就是考虑什么时候能从起点到终点,这道题很有意思的就是它宽度只有2,当且仅当一个块与其对着的三个块都不同时不可以通过时,即不形成墙,才可以走到,所以维护这个就好。
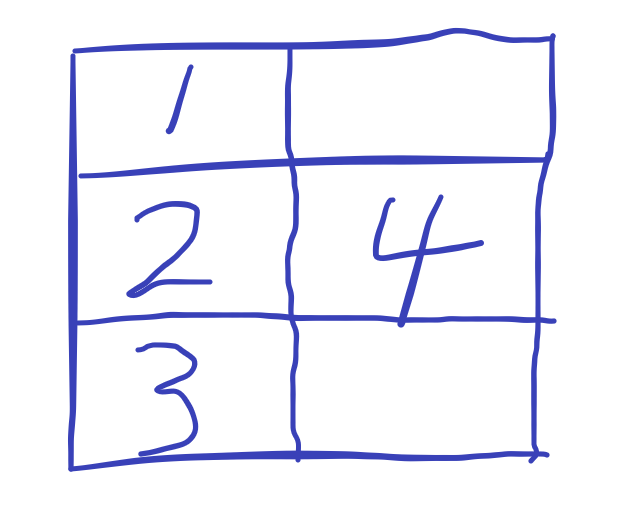
也就是说,当修改4时,分别判断一下1,2,3就好了,这样的话可以做到(O(M))的时间复杂度,可以过。
下面讨论一下这种做法的正确性,当1-4,3-4,2-4都形成墙时,说明至少要拆三次才能通过,而拆除任意一堵墙都不能使其联通,故至少要拆三次,其他情况同理。
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int q[2][N];
inline int read(){
int x=0;
char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch<='9'&&ch>='0'){
x=x*10+ch-'0';
ch=getchar();
}
return x;
}
int main(){
int cnt=0;
int n=read(),m=read();
while(m--){
int a=read(),b=read();
a--;
if(q[a][b]){
if(q[a^1][b-1])cnt--;
if(q[a^1][b])cnt--;
if(q[a^1][b+1])cnt--;
}else {
if(q[a^1][b-1])cnt++;
if(q[a^1][b])cnt++;
if(q[a^1][b+1])cnt++;
}
q[a][b]^=1;
if(cnt)cout<<"No"<<'
';
else cout<<"Yes"<<'
';
}
}