二叉搜索树的深度与搜索效率
二叉搜索树也可称为二叉查找树,它的常用方法可以参考:二叉查找树
我们在树, 二叉树, 二叉搜索树中提到,一个有n个节点的二叉树,它的最小深度为log(n),最大深度为n。比如下面两个二叉树:
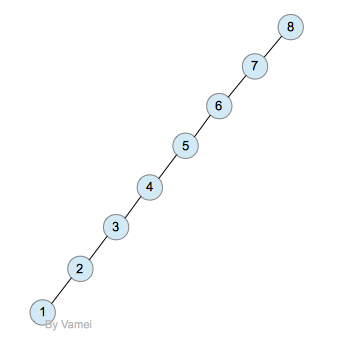
深度为n的二叉树
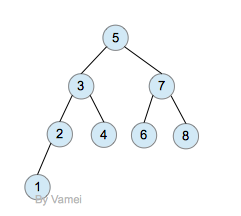
深度为log(n)的二叉树
这两个二叉树同时也是二叉搜索树(参考树, 二叉树, 二叉搜索树)。注意,log以2为基底。log(n)是指深度的量级。根据我们对深度的定义,精确的最小深度为floor(log(n)+1)。
我们将处于同一深度的节点归为一层。如果除最后一层外的其他层都被节点填满时,二叉树有最小深度log(n)。
二叉搜索树的深度越小,那么搜索所需要的运算时间越小。一个深度为log(n)的二叉搜索树,搜索算法的时间复杂度也是log(n)。然而,我们在二叉搜索树中已经实现的插入和删除操作并不能让保持log(n)的深度。如果我们按照8,7,6,5,4,3,2,1的顺序插入节点,那么就是一个深度为n的二叉树。那么,搜索算法的时间复杂度为n。
n和log(n)的时间复杂度意味着什么呢?时间复杂度代表了完成算法所需要的运算次数。时间复杂度越小,算法的速度越快。
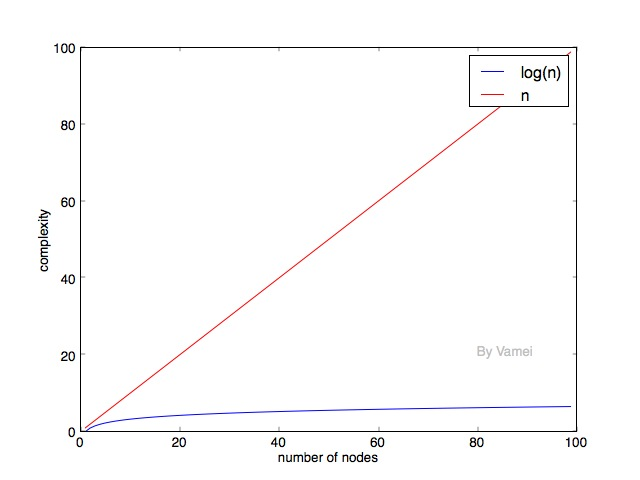
可以看到,随着元素的增加,log(n)的时间复杂度的增长要远小于n。所以,我们自然希望二叉搜索树能尽可能保持log(n)的深度。在上面深度为n的例子中,我们发现,每个节点只有左节点被填满。树的每一层都有很多空位。能不能尽可能减少每一层的空位呢? (相应的,减少树的深度)
“紧致”的树
一种想法是先填满一层,再去填充下一层,这样就是一个完全二叉树(complete binary tree)。这样的二叉树实现插入算法会比较复杂。我们将介绍一种思路相似,但比较容易实现的树状数据结构——AVL树。