编译器实现（四）

1.自顶向下的分析

参考：https://blog.csdn.net/hjc256/article/details/87949500

自顶向下的分析算法通过在最左推导中描述出各个步骤来分析记号串输入。

分析树隐含的编号是一个前序编号，顺序是由根到叶。

自顶向下的分析程序有两类：回溯分析程序，预测分析程序。

 

1.1使用递归下降分析算法进行自顶向下的分析

 1.1.1递归下降分析的基本方法

概念：

　　将一个非终结符A的文法规则看作将识别A的一个过程的定义。

 递归下降分析程序由一组过程组成，每个非终结符号有一个对应的过程。程序的执行从开始符号对应的过程开始，如果这个过程的过程体扫描了整个输入串，他就停止执行并宣布语法分析完成。

当非终结符有多个产生式时，可能需要回溯，即重复扫描。

产生式：

　　A→a | b | . . .

若a，b均为非终结符时，需要计算a，b的First集合，来确定何时使用A→a或A→b。

产生式：

　　A→ε

需要了解什么记号可以正规地出现在非终结符A之后，这个集合为Follow集合。

进行First集合和Follow集合的计算是为了对早期错误进行探测。

1.2 LL（1）分析

1.2.1 LL(1)文法

参考：https://blog.csdn.net/jxch____/article/details/78693775

第一个L表示从左向右扫描输入，第二个L表示产生最左推导，而“1”表示在每一步中只需要向前看一个输入符号来决定语法分析的动作。

文法G是LL(1)的，当且仅当对于G的每个非终结符Α的任何两个不同产生式
Α→α,Α→β均满足下面条件(其中α和β不能同时推出ε):
1、FIRST(α)∩FIRST(β)=Φ
2、假若β=>*ε，那么FIRST(α)∩FOLLOW(A)＝Φ

LL(1)分析使用显示栈来完成分析。

例：（LL(1)）分析的基本方法）

　　对文法：S→ (S) S | ε

　　

　　　　　　　　　　　　　　　　　　　自顶向下的分析动作

1.2.2 LL(1)分析与算法

构造一个LL(1)分析表表达出可能的自顶向下分析选择，这个表称为M[N,T]。N是文法的非终结符的集合，T是终结符或记号的集合（禁止将ε加入）。

构造规则：

　　1) 如果A→α是一个产生式选择，且有推导 α ⇒ *ab成立，其中a 是一个记号，则将A→a添加到表项目M [A, a] 中。

　　2) 如果A→α是一个产生式选择，且有推导 α⇒ *ε 和 S $ ⇒*βAaγ成立，其中S是开始符号，α是一个记号（或$），则将A→α添加到表项目M [A, a]中。

例： （LL(1)分析表）

　　对文法：S→ (S) S | ε

　　

定义：如果文法G相关的LL(1)分析表的每个项目中至多只有一个产生式，则该文法就是LL(1)文法(LL(1) grammar)。

利用LL(1)文法表构造出一个无二义性的分析。

1.2.3 消除左递归和提取左因子

将BNF表示法中的文法重写到LL (1)分析算法所能接受的格式上。应用的两个标准技术是左递归消除（left recursion removal）和提取左因子（left factoring）。这两个技术无法保证可将一个文法变成LL(1)文法，这就同EBNF一样无法保证在编写递归下降程序中可以解决所有的问题。

1.左递归消除

　　左递归被普遍地用来运算左结合。

　　（1）简单直接左递归

　　　　　　A→Aα | β

　　　　其中α和β是终结符和非终结符的串，而且β不以A开头。

　　　　重写规则：一个是首先生成β，另一个是生成α的重复，它不用左递归却用右递归：

　　　　　　A →βA^’

　　　　　　A^’ →αA^’ | ε

　　（2）普遍的直接左递归

　　　　　　A → Aα₁ | Aα₂ | . . . | Aα_n| β₁ | β₂ | . . . | β_n

　　　　　　其中β₁ ,β₂  . . .  β_n均不以A开头。

　　　　　　重写规则：

　　　　　　　　A →β₁ A^’| β₂ A^’ | . . . | β_m A’

　　　　　　　　A^’ →α₁A^’| α₂A^’ | . . . | α_n A^’ |ε

　　（3）一般的左递归

　　　　待写。。。

2.提取左因子

　　当两个或更多文法规则选择共享一个通用前缀串时，需要提取左因子。

　　A→αβ | αγ

　　重写规则：

　　A →αA^’ 

　　A^’  → β | γ

1.2.4 在LL(1)分析中构造语法树

主要原因却是分析栈所代表的仅是预测的结构，而不是已经看到的结构。因此，语法树节点的构造必须推迟到将结构从分析栈中移走时，而不是当它们首次被压入时。一般而言，这就要求使用一个额外的栈来记录语法树节点，并在分析栈中放入“动作”标记来指出什么动作何时将在树栈中发生。

例：E → E + n | n

　　重写：

　　E → n E^’

　　E’ → + n E^’ | ε
 　　

　　

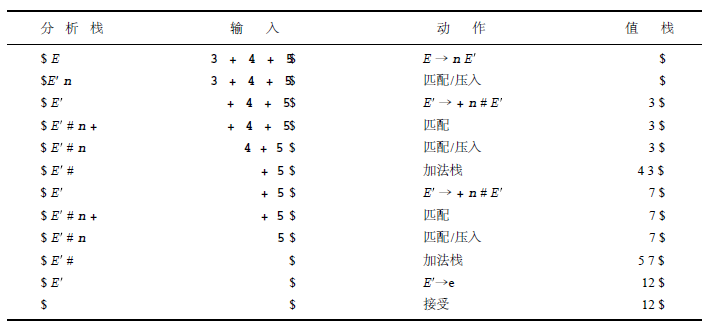
1.2 First集合和Follow集合

1.2.1 First集合

定义：令X为一个文法符号（一个终结符或非终结符）或，则集合First (X) 由终结符组成，此外可能还有ε，它的定义如下：

　　1. 若X是终结符或，则First (X) = {X}。

　　2. 若X是非终结符，则对于每个产生式X→X1X2 . . . Xn ，First (X)都包含了First(X1 ) - { ε}。若对于某个i < n，所有的集合First (X1 ), . . . , First 　　(Xi ) 都包括了ε，则First (X) 也包括了First (Xi + 1) - {ε }。若所有集合First (X1 ), . . . , First (Xn)包括了ε，则First (X)也包括ε。

　　

　　　　

1.2.3 Follow集合

定义：给出一个非终结符A，那么集合Follow (A)则是由终结符组成，此外可能还有$。
集合Follow (A)的定义如下：
　　1. 若A是开始符号，则$就在Follow (A)中。
　　2. 若存在产生式B→αAγ，则First (γ) - {ε}在Follow (A)中。
　　3. 若存在产生式B→αAγ，且ε在First (γ)中，则Follow (A)包括Follow (B)。

　　　　

1.2.4 构造LL(1)分析表

参见1.2.2中LL(1)分析表：

　　1) 如果A→α是一个产生式选择，且有推导 α ⇒ *αβ成立，其中α 是一个记号，则将A→α添加到表项目M [A, α] 中。

　　2) 如果A→ε是ε产生式选择，且有推导 S$ ⇒*αAα β 成立，其中S是开始符号，α是一个记号（或$），则将A→ε 添加到表项目M [A, a]中。

规则1中的记号 α很明显是在First (α) 中，且规则2的记号α 是在Follow (A)中，因此，就可得到LL(1) 分析表的以下算法构造：

LL(1) 分析表M[N, T] 的构造：为每个非终结符A和产生式A→α重复以下两个步骤：

　　1) 对于First (α)中的每个记号α，都将A→α添加到项目M [A, a]中。

　　2) 若ε在First (α)中，则对于Follow (A) 的每个元素α（记号或是$），都将A→α 添加到M[A, a]中。

LL(1)文法的判定规则：

　　定理：若满足以下条件，则B N F中的文法就是L L(1)文法（LL(1) grammar）。

　　　　1. 在每个产生式A→a1 | a2 | . . . |an 中，对于所有的 i 和 j：1≤i，j≤n，i≠j，First (ai ) ∩ First (aj )为空。

　　　　2. 若对于每个非终结符A都有First (A) 包含了 ε，那么First (A) ∩ Follow (A)为空。