Dijkstra 的两种算法

第一种算法的伪代码来自：https://www.bilibili.com/video/BV1Ut41197ae?from=search&seid=7706418527991382536  

========== 第一种算法

一，把 点集 分成两组

(1) S：已求出的最短路径的点的集合

(2) T = V - S：尚未确定的点的集合

保证：

①，从源点 V0 到 S 中各点的 最短路径 的长度都不大于从

V0 到 T 中任何点的最短路径长度

②，每点赋予一个值 

S：从 V0 到此点 最短路径长度

T：从 V0 到此点 只包括 S 中的点作中间点 的最短路径长度

另外，S  和 T  中点的 长度都用 数组D 存

二，步骤

1，初始化

S={ V0 }，T={ 其他点 }

D[ i ] 初值：若< V0,Vi > 存在，则为其权值，否则 为  无穷大

即：找出 源点V0 到 各点的直达路径，即只通过一条弧就 到达的路径

2，选择：从这些路径中找出一条最短路径 (V0,Vi) ,并将 Vi 加入 S

3，更新 

对 T 中 点的距离 进行修改：若加入 Vj 作为 中间点，使得 V0 Vj Vi 小于 V0 Vi,

则修改距离值。

4，重复 2，3 操作，直到 S = V

三，例题

1，

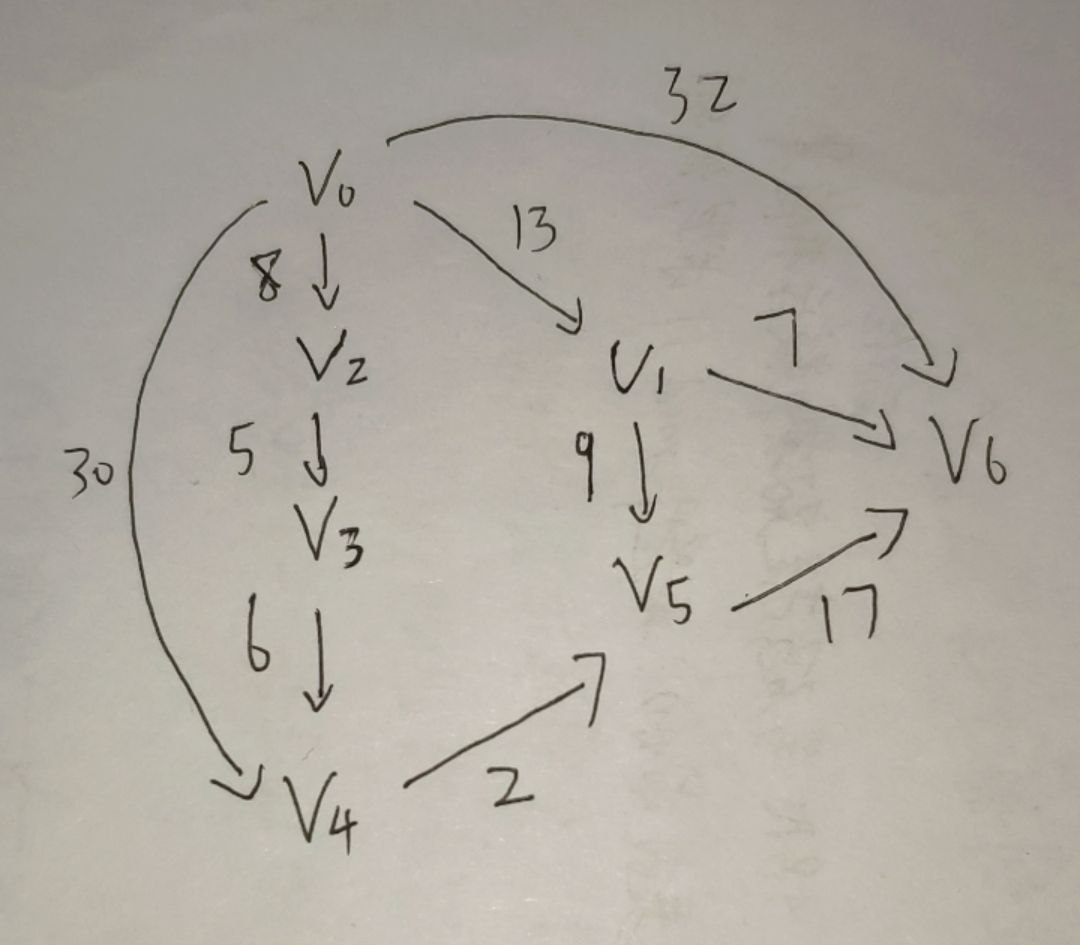
2，其实我们书本上的和这个差不多原理，不过看你起来更简洁

 四，代码

1，这个代码完全是按照上面的步骤，其中的测试数据 亦是上面例题的第一题的那种画法

其实 真的可以画一下那个表格，步骤一模一样

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define MIN(x,y) (((x)<(y))?(x):(y));
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x3f3f3f3f
#define N 1005
#define M 100005
int a[N][N];  // 存边
int dis[N];  // 刚开始是存 T中点的长度，然后到最后变成 源点到各点的最短距离
bool vis[N];  // 标记 点 是否已经加入 S 中
int p[N];   // 存路径
int n, m;  // n 是点数，m 是边数，
void init()
{
    mem(p, 0);
    mem(vis, 0);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (a[i][j] == 0)
                a[i][j] = inf + 1;    // 不存在这条边
        }
    }
}
void dij(int src)
{
    init();
    vis[src] = 1;
    for (int i = 0; i < n; i++)  // 1,  初始化 即找出 源点V0 到 各点的直达路径    
    {
        dis[i] = a[src][i];
        p[i] = src;
    }
    p[src] = -1;

    for (int i = 1; i < n; i++)  // 4，重复 2，3 操作，直到 S = V （把 S=V 换成确定的循环次数，除 源点 不用找最短路径，其他都要
    {
        int min = inf, kmin = src;
        for (int j = 1; j < n; j++) // 2，选择：从这些路径中找出一条最短路径 (V0,Vi) ,并将 Vi 加入 S
        {
            if (vis[j] == 1)   // 判断 这点 是否在 S 中，即 这点的最短路径 是否确定
                continue;
            if (min > dis[j])
            {
                min = dis[j];
                kmin = j;
            }
        }
        vis[kmin] = 1;    // 标记确定的点，即 将 点 加入 S 中

        for (int j = 1; j < n; j++)  //3，更新 对 T 中 点的距离 进行修改：若加入 Vj 作为 中间点，使得 V0 Vj Vi 小于 V0 Vi,则修改距离值。
        {
            if (vis[j] == 1)
                continue;
            if (dis[j] > dis[kmin] + a[kmin][j])
            {
                p[j] = kmin;
                dis[j] = dis[kmin] + a[kmin][j];
            }
        }
    }
}
void show(int end)
{
    if (p[end] != -1)
        show(p[end]);
    if (p[end] == -1)
        printf("%d", end);
    else
        printf("->%d", end);
}
int main(void)
{
    int i, j, w;
    scanf("%d%d", &n, &m);
    for (int k = 0; k < m; k++)
    {
        scanf("%d%d%d", &i, &j, &w);
        a[i][j] = w;
    }
    dij(0);

    for (int i = 1; i < n; i++)
    {
        printf("%d ", dis[i]);
    }puts("");

    printf("起点 到 v4 最短路径路线：");
    show(4);
    puts("");
    printf("起点 到 v6 最短路径路线：");
    show(6);
    puts("");

    system("pause");
    return 0;
}
/*
7 10
0 2 8
2 3 5
3 4 6
0 4 30
0 1 13
1 6 7
1 5 9
4 5 2
5 6 17
0 6 32
*/

============= 第二种算法

是用优先队列做的，这里不多解释。 之前我有讲过，可以移步  https://www.cnblogs.com/asdfknjhu/p/12538668.html

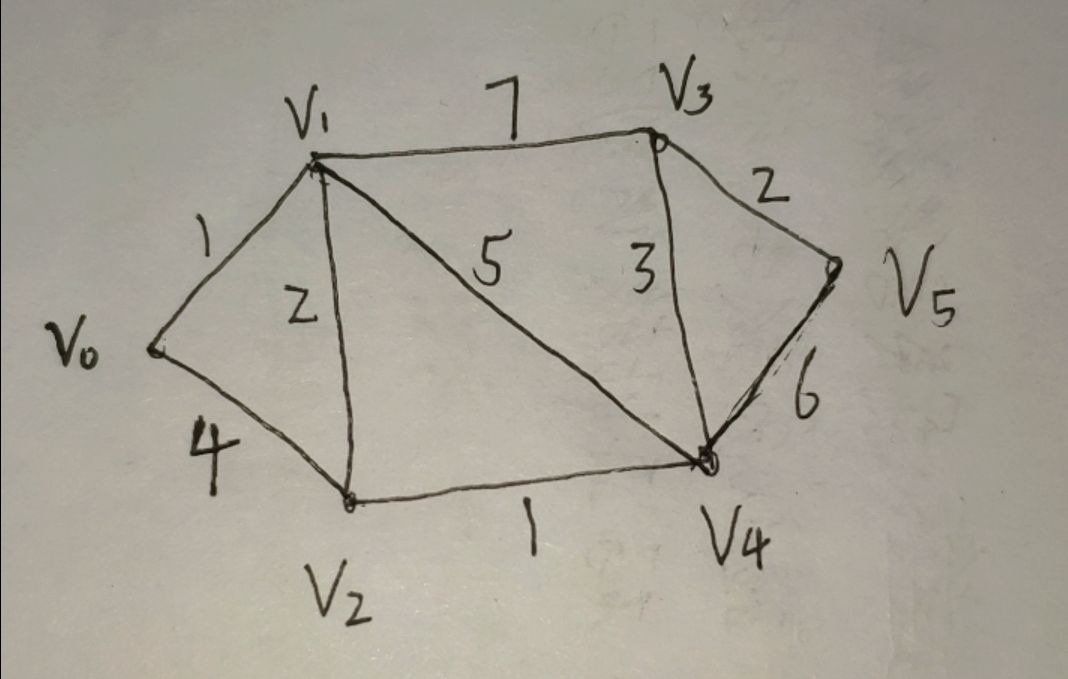
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<queue>
using namespace std;
#define N 100
typedef struct  Edge
{
    int to;
    int w;
    int pre;
}eg; eg e[N];
typedef struct node    // 队列里要放的应该是 点的 id 和 distance ，而不是一条边
{
    int id;
    int dis;
    node() {}
    node(int  a, int b) :id(a), dis(b) {}
    friend bool operator <(const node &a,const node &b)  // < 的重载
    {
        return a.dis > b.dis;
    }
}st;
/*
typedef struct node    // 队列里要放的应该是 点的 id 和 distance ，而不是一条边
{
int id;
int dis;
node() {}
node(int  a, int b) :id(a), dis(b) {}
bool operator <(const node &a)const  // < 的重载
{
return a.dis < dis;
}
}st;*/
int tot = 0, last[N], vis[N];
int dist[N], p[N];   // 记录距离和前一个点的 id
void add(int from, int to, int w)
{
    tot++;
    e[tot].to = to;
    e[tot].w = w;

    e[tot].pre = last[from];
    last[from] = tot;
}
void Dijkstra(int start)
{
    priority_queue <st>q;   // 小于号的重载是对于优先队列 来说
    q.push(st(start, 0));  // 起点为 1
    dist[start] = 0, p[start] = -1;
    while (q.size())
    {
        st vertex = q.top();
        q.pop();
        vis[vertex.id] = 1;  // 出栈的时候标记

        for (int i = last[vertex.id]; ~i; i = e[i].pre)  //遍历这个点相邻的边
        {
            st next = { e[i].to,e[i].w + vertex.dis };
            if (vis[next.id] == 0)//如果下一个点还没有走过
            {
                if (dist[next.id] > next.dis)    //如果新来的点距离更近 更新 距离和前一个点的 id,
                {
                    p[next.id] = vertex.id;
                    dist[next.id] = next.dis;
                    q.push(next);
                }
            }

        }
    }
}
void show(int end)
{
    if (p[end] != -1)
        show(p[end]);
    printf("%d ", end);
}
int main(void)
{
    int n; scanf("%d", &n);
    memset(last, -1, sizeof(last));
    memset(vis, 0, sizeof(vis));
    memset(dist, 0x3f, sizeof(dist));
    tot = 0;

    while (n--)
    {
        int from, to, w;  // 起点 终点 权值
        scanf("%d%d%d", &from, &to, &w);
        add(from, to, w);
        add(to, from, w);  // 无向图
    }
    Dijkstra(1);  // 起点
    printf("路线：");
    show(6); //终点
    printf("
距离：%d
", dist[6]);

    system("pause");
    return 0;
}
/* 测试数据
8
1 2 5
1 3 1
2 3 2
2 4 1
3 4 4
3 5 8
4 5 3
4 6 6

*/

 最后总结一下，这个是看书的，我可不懂这些

第一种： 用 邻接矩阵 存图，这里邻接矩阵适合 点少边多的稠密图。 但这种算法适合 点多边少的稠密图，复杂度 O ( V*V)

第二种：用 链式前向星 存图 (书里用邻接表，不过我感觉差不多，不太确定)。这种算法 适合 边少点多的稀疏图，复杂度 O ( V + E logV )

 ========= ======== ======== ====== ====== ===== ==== === == =

人没有牺牲就什麽都得不到，为了得到什麽东西，就需要付出同等的代价。  

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　—— 钢炼