! JSOI2014士兵部署——点到凸包的切线

给定n个整点，q次询问（独立），每次询问加入一个整点后，凸包的面积，(n,qleq1e5)

前置芝士

凸包的极值点

如图可见凸包在u方向上的极值点

考虑二分，当前区间([a,b])，c为中间点，将问题缩至一半

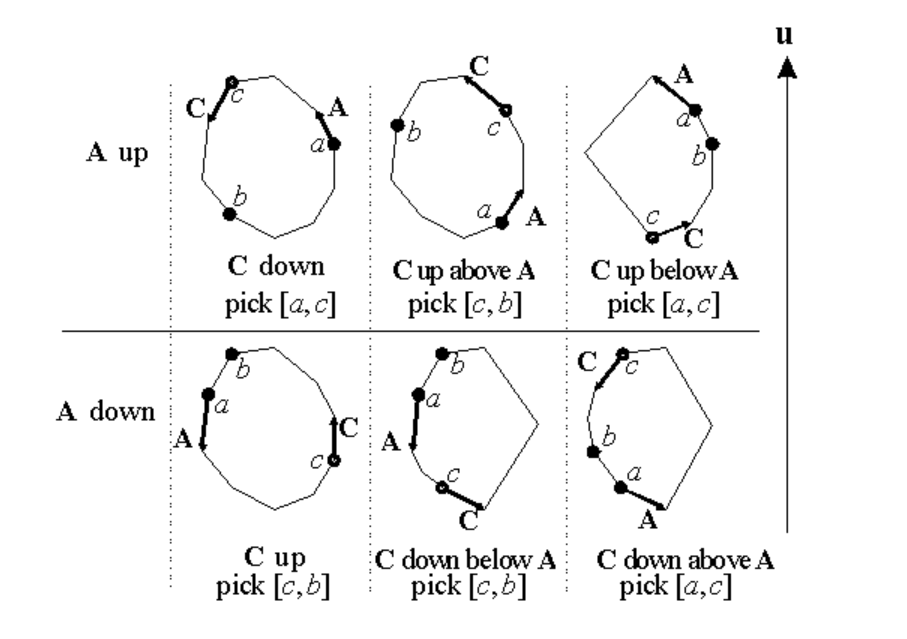
按照上图讨论即可（边都是逆时针）

若经过c的边，先上升后下降说明我们已经找到了一个最大值

点到多边形的切线

我的想法(O(n))

询问离线，以凸包内一点给点极角排序，那么在同一条线上的点的切点是相同的

像旋转卡壳一样，随着查询点逆时针旋转，切点也逆时针旋转

二分方法(O(nlogn))

定义边e是向上的->p在e的右边，这样就可以用刚才的求凸包极值点的算法解决

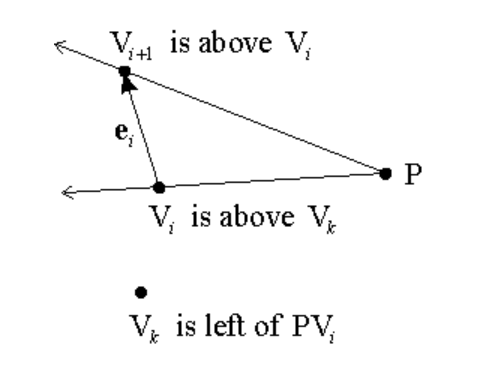
回到题目

首先log判点是否在凸包内

右下角连线把凸包分为n-2个三角形，二分tan在哪个三角形tan区域内，然后叉积判一下在不在三角形内

算切线，减去中间一块的面积（前缀和），再加上新的即可

CODE：

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
	int x=0,f=1;char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f==1?x:-x;
}
const int N=1e5+4;
struct poin{
	int x,y;
	inline poin operator -(const poin &a)const{
		return (poin){x-a.x,y-a.y}; 
	}
	inline int operator *(const poin &a)const{
		return x*a.y-y*a.x;
	}
}a[N],q;
inline bool up(int i){
	return (a[i+1]-q)*(a[i]-q)>0;
}
inline bool above(int i,int j){
	return (a[i]-q)*(a[j]-q)>0;
}
int n,Q,top,s[N];
double th[N];
inline bool in(){
	double al=atan2(q.y-a[1].y,q.x-a[1].x);
	if(al<th[2]||al>th[n])return 0;
	int x=lower_bound(th+2,th+n+1,al)-th;
	return (a[x-1]-q)*(a[x]-q)>=0;
}
inline void solve(){
	q.x=read();q.y=read();
	static int l,r,mid,ans,qmx,qmn;
	if(in()){
		ans=s[n];
		if(ans&1)cout<<ans/2<<".5
";
		else cout<<ans/2<<".0
";
		return;
	}
	l=1;r=n;
	while(l<r){
		mid=l+r>>1;
		if(up(mid-1)&&!up(mid)){qmx=mid;break;}
		if(mid<n&&up(mid)&&!up(mid+1)){qmx=mid+1;break;}
		if(up(l)){
			if(!up(mid))r=mid;
			else if(above(mid,l))l=mid;
			else r=mid;
		}
		else{
			if(up(mid))l=mid;
			else if(above(mid,l))r=mid;
			else l=mid;
		}
	}
	l=1;r=n;
	while(l<r){
		mid=l+r>>1;
		if(!up(mid-1)&&up(mid)){qmn=mid;break;}
		if(mid<n&&!up(mid)&&up(mid+1)){qmn=mid+1;break;}
		if(!up(l)){
			if(up(mid))r=mid;
			else if(!above(mid,l))l=mid;
			else r=mid;
		}
		else{
			if(!up(mid))l=mid;
			else if(!above(mid,l))r=mid;
			else l=mid;
		}
	}
	if(qmn<=qmx)ans=s[n]-s[qmx-1]+s[qmn-1];
	else ans=s[n]-s[qmx-1]+s[qmn-1];
	ans+=a[qmn]*q+q*a[qmx];
	if(ans&1)cout<<ans/2<<".5
";
	else cout<<ans/2<<".0
";
}
inline bool comp(const poin &e,const poin &f){
	int x=(e-a[1])*(f-a[1]);
	return x==0?e.x<f.x:x>0;
}
signed main(){
	n=read();Q=read();
	for(int i=1;i<=n;i++){
		a[i].x=read();a[i].y=read();
	} 
	for(int i=2;i<=n;i++)
		if(a[i].y<a[1].y||(a[i].y==a[1].y&&a[i].x<a[1].x))swap(a[i],a[1]);
	sort(a+2,a+n+1,comp);
	for(int i=1;i<=n;i++){
		while(top>1&&(a[i]-a[top-1])*(a[top]-a[top-1])>=0)top--;
		a[++top]=a[i];
	}
	n=top;a[0]=a[n];a[n+1]=a[1];
	for(int i=1;i<=n;i++)
		s[i]=s[i-1]+a[i]*a[i+1]; 
	for(int i=2;i<=n;i++)
		th[i]=atan2(a[i].y-a[1].y,a[i].x-a[1].x);
	while(Q--)solve();
	return (0-0);
}