第一种方法
#计算 弹性模量
设置:
晶格类型:diamond
晶格常数:3.567 A
region box block 0 20 0 20 0 20 units lattice
create_box 1 box
create_atoms 1 box
势:
pair_style tersoff
pair_coeff * * SiC.tersoff C
每步的修正:
fix 1 all deform 1 z delta 0.0 0.21402 units box
运行lammps:
提取出每次修正的初始能量:(附上 python 数据提取代码)
def read(path):
b=2
f=open(path)
fw=open(path+'.output','w')
for line in f.readlines():
b=b+1
if 'Energy initial' in str(line):
b=0
if b==1:
print(line)
fw.write(line)
提取的数据如下:
-471563.715475 -471563.715475 -471563.715475
-471559.573965 -471559.573965 -471559.573967
-471549.996058 -471549.996058 -471549.996058
-471535.007192 -471535.007192 -471535.007192
-471514.632964 -471514.632964 -471514.632964
-471488.899114 -471488.899114 -471488.899114
-471457.831529 -471457.831529 -471457.831529
-471421.456236 -471421.456236 -471421.456236
-471379.799399 -471379.799399 -471379.799399
-471332.887319 -471332.887319 -471332.887319
-471280.746425 -471280.746425 -471280.746425
-471223.403279 -471223.403279 -471223.403279
-471160.884564 -471160.884564 -471160.884564
-471093.217089 -471093.217089 -471093.217089
-471020.427778 -471020.427778 -471020.427778
-470942.543674 -470942.543674 -470942.543674
-470859.59193 -470859.59193 -470859.59193
-470771.599811 -470771.599811 -470771.599811
-470678.594686 -470678.594686 -470678.594686
-470580.604026 -470580.604026 -470580.604026
-470477.655406 -470477.655406 -470477.655406
只取第一列数据:
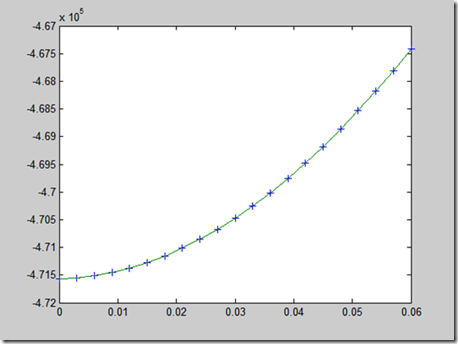
并绘制 能量-应变 曲线:
Matlab 五次多项式拟合:
Linear model Poly5:
f(x) = p1*x^5 + p2*x^4 + p3*x^3 + p4*x^2 + p5*x + p6
Coefficients (with 95% confidence bounds):
p1 = 3.509e+06 (3.507e+06, 3.51e+06)
p2 = -1.294e+06 (-1.294e+06, -1.294e+06)
p3 = -1.245e+06 (-1.245e+06, -1.245e+06)
p4 = 1.214e+06 (1.214e+06, 1.214e+06)
p5 = 943.2 (943.2, 943.2)
p6 = -4.716e+05 (-4.716e+05, -4.716e+05)
Goodness of fit:
SSE: 2.548e-10
R-square: 1
Adjusted R-square: 1
RMSE: 4.122e-06
二次项系数:1.214e+06
>>> Vc=3.567**3*20**3
>>> C2=1.214e+06
>>> C11=2*C2/Vc/6.2415e-3
>>> C11
1071.4215876370854
同样也可以计算C12=101.7246
体弹性模量:B=1/3(C11+2*C12)=424.9569
第二种方法: