监督学习的回归问题上做了介绍,讲解的是房价问题:
采用的代价函数为全局的误差计算,并将计算的参数结果同时更新,为批梯度下降法。

批梯度下降法在多个参数时的运算过程:

有时候,为了让数据的影响程度,或者说是具有一致性,需要数据预处理,集中在均值0附件即可

在学习率问题上,采用倍数为3从0.001处开始进行的尝试,是一种确定最佳学习率的方案。学习率过小只是需要更多的迭代次数,而过大则会导致误差变大然后失去学习能力,反复变化学习误差等。

有些输入数据与输出数据在进行映射时,应该考虑数据的联合意义如:房价和房宽与房长:

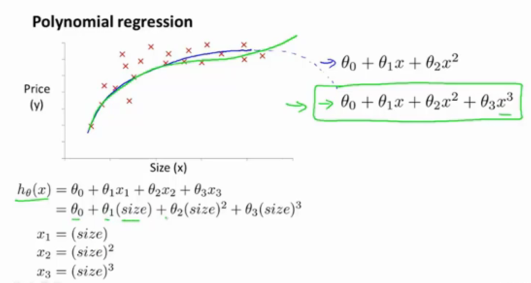
在有些数据映射时,如果在数据点图中,已经呈现出了一定的关系,可以使用同一变量的高次函数进行拟合,并通过事先的考虑,该高次函数能否正确映射到图中:
对于输入X特征,输出Y的实际结果,对应的系数A可以直接求解而不用梯度下降:(都是矩阵向量)
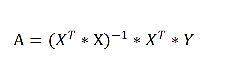
在m训练样本,n特征的回归问题上,梯度下降和使用矩阵运算直接求最终值时,各有优缺点。特征数量n小于1万,还是建议直接用正常的矩阵运算,虽然复杂度为n3:

有时候(很少)不能进行矩阵逆运算的问题:特征之间有联系,多余的特征,或者样本数量很少但是特征却很多很多:
