分析树

分析树

Python 

分析树

如何使用树来解决一些真正的问题？

分析树可以用于表示诸如句子或数学表达式的真实世界构造。

 

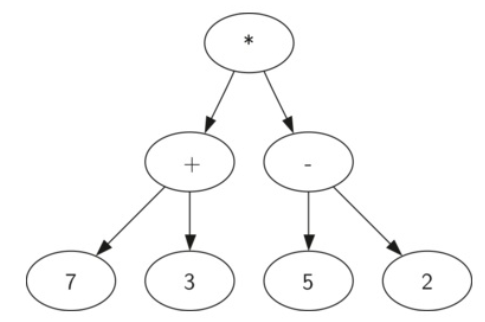
数学表达式的分析树

 

上图表示诸如 （（7 + 3）*（5-2））数学表达式作为分析树。

构建分析树

构建步骤

1. 第一步是将表达式字符串拆分成符号列表。
2. 有四种不同的符号要考虑：左括号，右括号，运算符和操作数。
3. 每当我们读一个左括号，我们开始一个新的表达式，因此我们应该创建一个新的树来对应于该表达式。
4. 每当我们读一个右括号，我们就完成了一个表达式。
5. 每个操作符都将有一个左和右孩子。

定义规则

• 如果当前符号是 '(' ，添加一个新节点作为当前节点的左子节点，并下降到左子节点。
• 如果当前符号在列表 ['+'，' - '，'/'，'*'] 中，请将当前节点的根值设置为由当前符号表示的运算符。 添加一个新节点作为当前节点的右子节点，并下降到右子节点。
• 如果当前符号是数字，将当前节点的根值设置为该数字并返回到父节点。
• 如果当前符号是 ')' ，则转到当前节点的父节点。

构建实例

在编写 Python 代码之前，让我们看看上面列出的规则的一个例子。我们将使用表达
式 （3+（4 * 5） ） 。我们将把这个表达式解析成下面的字符标记列表
['('，'3'，'+'，'('，'4'，'*'，'5'，')'，')'] 。

1. 创建一个空树。
2. 读取 ( 作为第一个标记。按规则1，创建一个新节点作为根的左子节点。使当前节点到这个新子节点。
3. 读取 3 作为下一个符号。按照规则3，将当前节点的根值设置为3，使当前节点返回到父节点。
4. 读取 + 作为下一个符号。根据规则2，将当前节点的根值设置为+，并添加一个新节点作为右子节点。新的右子节点成为当前节点。
5. 读取 ( 作为下一个符号，按规则1，创建一个新节点作为当前节点的左子节点，新的左子节点成为当前节点。
6. 读取 4 作为下一个符号。根据规则3，将当前节点的值设置为 4。使当前节点返回到父节点。
7. 读取 作为下一个符号。根据规则2，将当前节点的根值设置为 ，并创建一个新的右子节点。新的右子节点成为当前节点。
8. 读取 5 作为下一个符号。根据规则3，将当前节点的根值设置为5。使当前节点返回到父节点。
9. 读取 ) 作为下一个符号。根据规则4，使当前节点返回到父节点。
10. 读取 ) 作为下一个符号。根据规则4，使当前节点返回到父节点 + 。没有 + 的父节点，所以我们完成创建。

从上面的例子，很明显，我们需要跟踪当前节点以及当前节点的父节点。

保持跟踪父对象的简单解决方案是使用栈。每当我们想下降到当前节点的子节点时，我们首先将当前节点入到栈上。当我们想要返回到当前节点的父节点时，我们将父节点从栈中弹出。

分析树构建代码

from pythonds.basic.stack import Stack
from pythonds.trees.binaryTree import BinaryTree


def buildParseTree(fpexp):
    # fplist = fpexp.split()
    fplist = [i for i in fpexp]
    # print(fplist)
    # exit()
    pStack = Stack()
    eTree = BinaryTree('')
    pStack.push(eTree)
    currentTree = eTree

    for i in fplist:
        if i == '(':
            currentTree.insertLeft('')
            pStack.push(currentTree)
            currentTree = currentTree.getLeftChild()
        elif i not in ['+', '-', '*', '/', ')']:
            currentTree.setRootVal(int(i))
            parent = pStack.pop()
            currentTree = parent
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i)
            currentTree.insertRight('')
            pStack.push(currentTree)
            currentTree = currentTree.getRightChild()
        elif i == ')':
            currentTree = pStack.pop()

        # 如果我们从列表中得到一个 token，引发一个ValueError异常。
        else:
            raise ValueError

    return eTree

评估分析树构建函数

在分析树中，叶节点将始终是操作数。

将函数移向基本情况的递归步骤是在当前节点的左子节点和右子节点上调用 evaluate 。递归调用有效地使我们沿着树向着叶节点移动。

运算符模块为我们提供了许多常用操作符的功能。当我们在字典中查找一个运算符时，检索相应的函数对象。由于检索的对象是一个函数，我们可以用通常的方式 function(param1，param2) 调用它。因此，查找 opers'+' 等效
于 operator.add(2,2) 。

评估函数代码

import operator


def evaluate(parseTree):
    opers = {'+': operator.add, '-': operator.sub, '*': operator.mul, '/': operator.truediv}
    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()

    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC), evaluate(rightC))
    else:
        return parseTree.getRootVal()