
背景
大家有没有考虑过,工作(编程)一段时间之后,我们都会出现技术上的瓶颈,怎么去突破?
我自身领悟到的是,除了抽象问题能力的提升外,如对问题宏观角度理解,还有很多是逻辑上的推理能力!
在日常工作中,我们有没有把系统功能往数学相关性上考虑呢?马克思一生也不断的在探索数学知识,在写资本论的时候,经常会从数学的角度考虑问题(有《马克思数学手稿》一书做凭证,这本书目前都成古董了,市面上很难买到)。
从现在开始,让我们融入数学的海洋中吧!一起去探讨学习数学知识。
序章
 函数是什么?
函数是什么?一件事变成了这样,使得另一件事变成了那样,所谓函数,说的就是事物间的相关性。
函数说到底就是用来描述“关系”(或“因果”)、“变化”或者“单位变化”的工具。
我们经常用的y=f(x)代表什么?
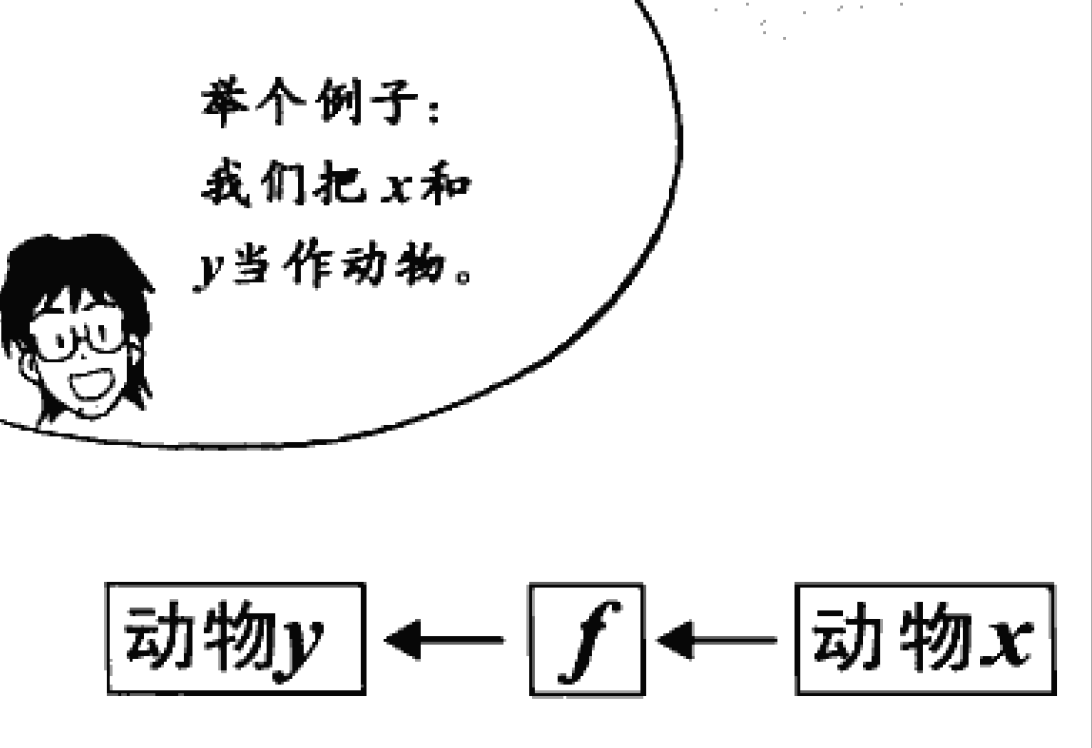
举个例子:把x当成青蛙,把青蛙放进一个f的盒子中,变换一下,就能出来一只叫y的蝌蚪。就是使用f给x施加某种规则或关系,进而推导出y。
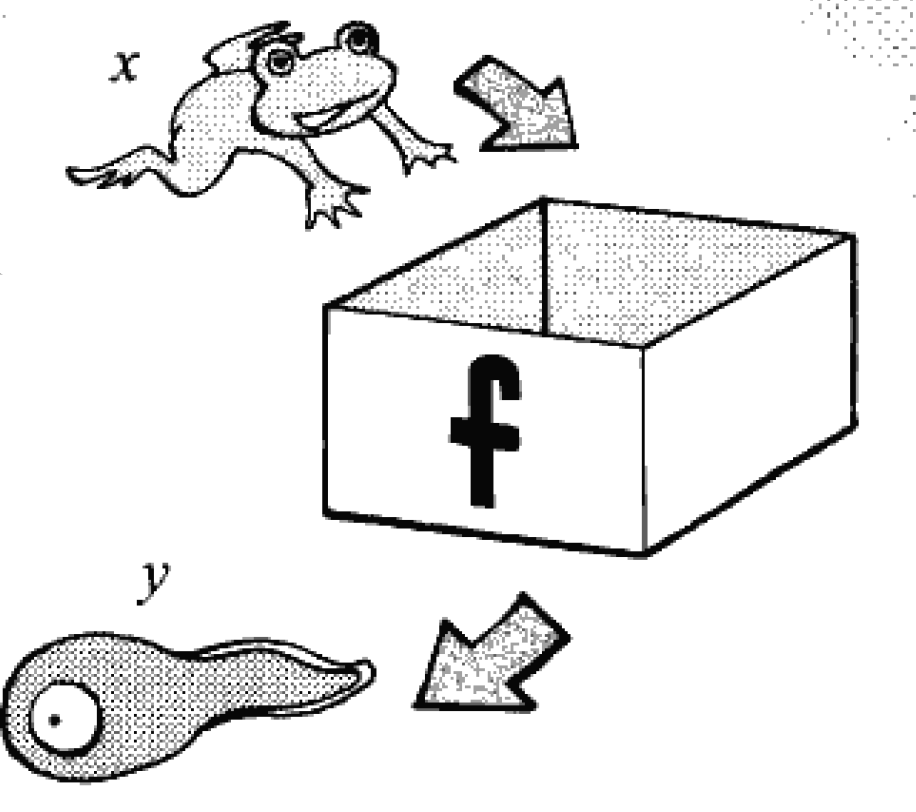
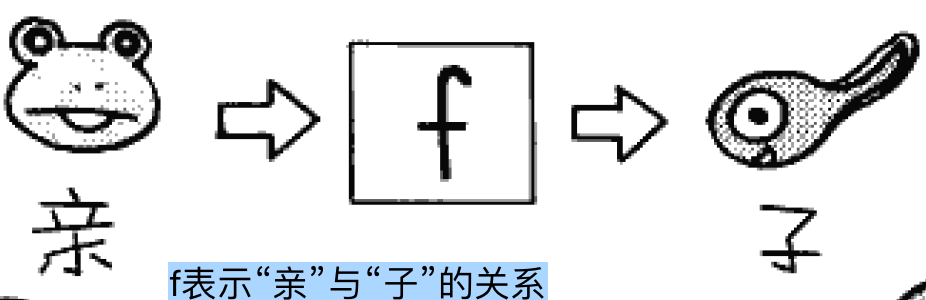

函数特征
因果
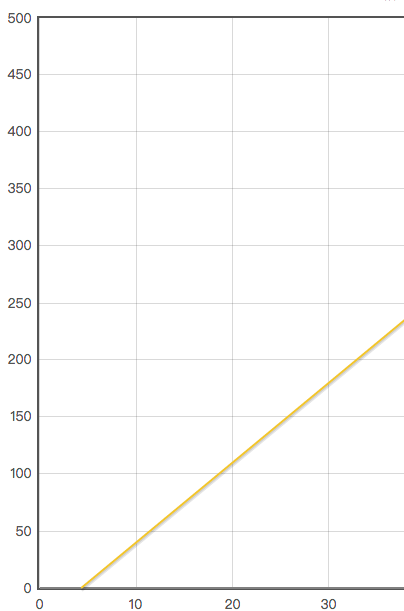
如:温度为x° C,蟋蟀1分钟鸣叫次数为y。可表示为: y = g(x) = 7 x - 30,当x = 30时, 有为 180。 即 1分钟鸣叫180次。
画成图形的话,就是一条直线:
单位变换
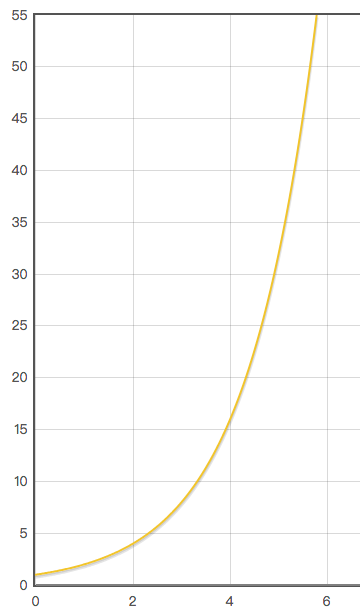
如:计算机采用经过二进制法(0, 1)处理后的信息,x比特锁表示的信息量为有,则 y = b(x) = 2 ^ x。
画成图形的话,就是指数函数。
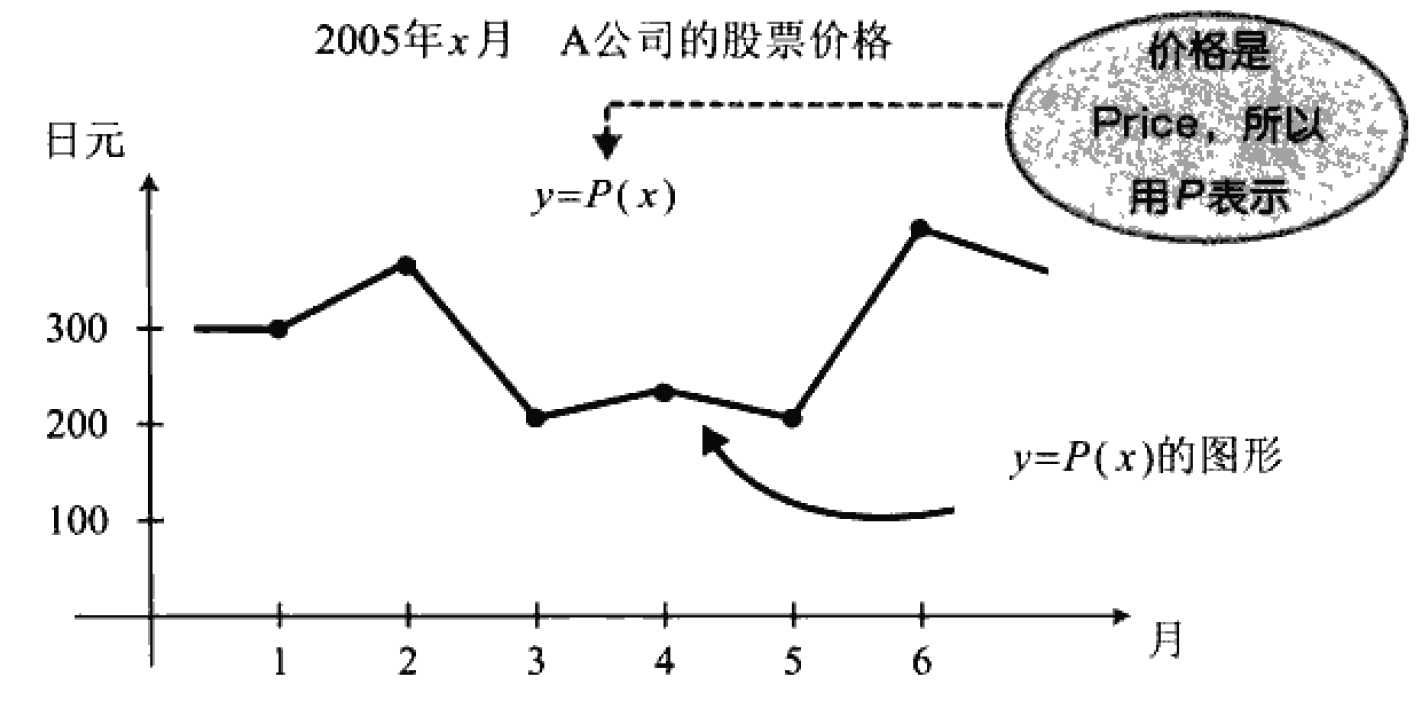
单位阶跃函数
如:A公司的股票价格,不能用一条直线或者特定形式的曲线来表示的函数。
函数如:
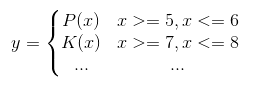
复合函数
函数组合在一起之后称为“复合函数”。我们能够通过复合函数将因果关系扩展到更广阔的范围。
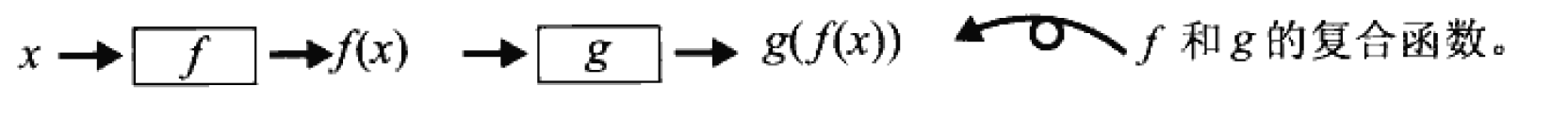
微分:就是将函数化繁为简

如果我们想知道目前国内通货膨胀情况,可以近似用下面函数去理解。
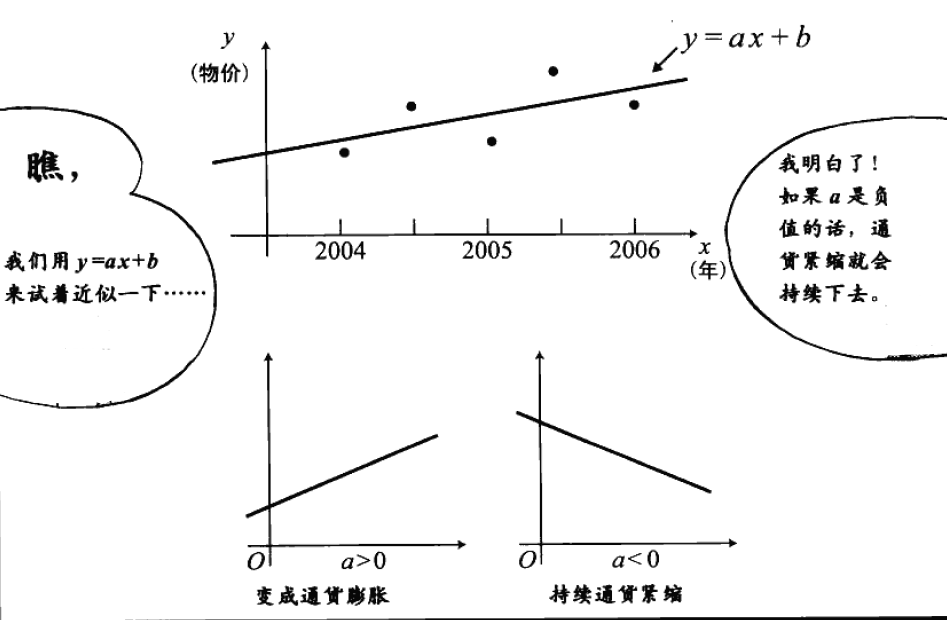
篇幅和时间所限,今天暂时写到这里,明天再续,有什么问题欢迎大家一起交流。
推荐
