链接:
http://codeforces.com/contest/601/problem/B
题意:
For an array 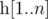 , we define it's Lipschitz constant
, we define it's Lipschitz constant 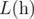 as follows:
as follows:
- if n < 2,
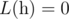
- if n ≥ 2,
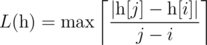 over all 1 ≤ i < j ≤ n
over all 1 ≤ i < j ≤ n
每次询问一个l,r, 求所有子串的h和
题解:
可以发现L(h)的最大值一定会是两个连续的ai的差的绝对值,这个可以用反证法来证明
所以我们先让a[i]=a[i+1]-a[i],然后对于每一个a[i],找出最左边不大于a[i]的下标,找出最右边小于a[i]的下标,这个可以用单调栈来求
询问的时候就遍历一下区间的每一个元素就可以了,这也是为什么q才100
代码:
31 int n, q; 32 int a[MAXN]; 33 int l[MAXN], r[MAXN]; 34 35 int main() { 36 ios::sync_with_stdio(false), cin.tie(0); 37 cin >> n >> q; 38 rep(i, 1, n + 1) cin >> a[i]; 39 rep(i, 1, n) a[i] = abs(a[i + 1] - a[i]); 40 rep(i, 1, n) l[i] = r[i] = i; 41 rep(i, 2, n) { 42 int now = i; 43 while (now > 1 && a[i] >= a[now - 1]) now = l[now - 1]; 44 l[i] = now; 45 } 46 per(i, 1, n - 1) { 47 int now = i; 48 while (now < n - 1 && a[i] > a[now + 1]) now = r[now + 1]; 49 r[i] = now; 50 } 51 while (q--) { 52 int beg, end; 53 cin >> beg >> end; 54 ll ans = 0; 55 rep(i, beg, end) { 56 int x = max(beg, l[i]); 57 int y = min(end - 1, r[i]); 58 ans += 1LL * (i - x + 1)*(y - i + 1)*a[i]; 59 } 60 cout << ans << endl; 61 } 62 return 0; 63 }