1. 重要概念
1.1 单调格式:
如果一个格式可以写成:(u_i^{n+1}=f(u_{i-p}^n,u_{i-p+1}^n, dots, u^n_{i+q}))的形式,并且对于每一个变元(u_k^n,k=i-p,i-p+1,dots,i+q)都有:
[frac{part f(u_{i-p}^n,u_{i-p+1}^n, dots, u^n_{i+q})}{part u_i^n}>0
]
则该格式为单调格式。
一个典型的例子是:
[u_i^{n+1}=sum_k a_ku_{j+k}^n
]
当组合系数为正时((a_k>0))为单调格式。
1.2 保单调格式
设n时刻({u_i^n})是单调的,如果通过某个格式,得到n+1时刻的({u_i^{n+1}})也是单调的,则该格式为保单调格式。
1.3 TVD格式
总变差定义为:(TV=sum_i|u_{i+1}-u_i|)。
TVD格式定义为:满足条件(TV^{n+1}le TV^n)的格式。
1.3.1 Harten定理
如果一个三点格式,可以写成:
[u^{n+1}_i=u^n_i+C(u_{i+1}^n-u_i^n)-D(u_i^n-u_{i-1}^n)
]
且:(Cge0,quad Dge 0, quad C+Dle1),则该格式为TVD格式。
1.3.2 构建TVD格式的思路
对原有格式进行改造:
原有格式=一阶迎风+修正项
TVD型格式=一阶迎风+限制器*修正项
限制器(psi=psi(r)),其中:
[r=frac{u_i-u_{i-1}}{u_{i+1}-u_{i}}
]
二阶精度范围:(1le psi(r) le r; 或者 r le psi(r)le 1);
TVD范围:(0lepsi(r) le min(2,2r));
如图:
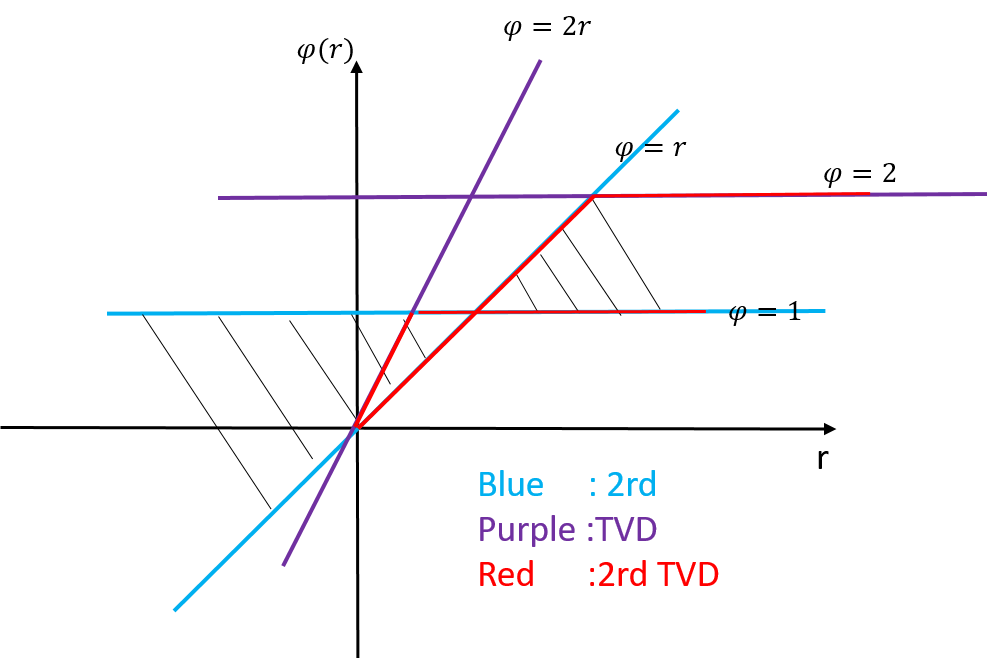
结论:
- 常系数的单调格式只能是一阶精度。
- 单调格式必是保单调格式。
- 保单调格式必是TVD格式。
- 对于线性格式(形如(u_i^{n+1}=sum_k a_ku_{j+k}^n)的格式),单调性和保单调性等价。