平面直角坐标系点坐标与多边形位置判断

　　受到在线变成QQ群讨论的一个问题启发，“如何判断点是否在三角形内部？”

　　给定一个平面直角坐标系和一组数据，数据由一系列坐标点组成，形式如：(x_i, y_i)，i = 1, 2, 3……, n; 给定的(x_i, y_i)可以组成一个封闭的多边形，数组下标顺序连接点坐标，(x₀, y₀) -> (x₁, y₁) -> ……->(x_n-1, y_n-1) ->(x₀, y₀)，现在给定一个坐标点(X, Y)，请判断该点的位置：返回 1 表示在多边形内部，返回 0 表示在多边形边上，返回 -1 表示在多边形外部。

 

思路1：分割法

         假设n = 3, (x_i, y_i)，i=1,2,3; 三个点坐标为(0, 0), (0, 1), (1, 0),那么该三角形围成的三条直线的解析式分别为：y = 0;  x = 0;  y = -x + 1；还记得高中时我们学的不等式方程吗，如图所示：

　　　

　　如果点(X₀, Y₀)在上图中封闭的三角形内部，那么满足三个不等式：

　　　　X₀ > 0; Y₀ > 0; X₀ + Y₀ -1 < 0; 若在三角形边上则是三个不等式转换为相应的等式：

　　　　X₀ = 0; Y₀ = 0; X₀ + Y₀ -1 = 0; 其余情况则是点在三角形外部；

      通过上面两个例子，解析式用a_ix_i + b_iy_i + c_i = 0表示，可以得到结论，则有当n 为3时，满足三个对应的不等式。

　　在解题的过程中，发现对于任意多边形来说，需要讨论的情况太复杂，所以在这里我们假设该多边形是一个凸多边形。所谓凸多边形，就是把一个多边形任意一边向两方无限延长成为一条直线，如果多边形的其他各边均在此直线的同旁，那么这个多边形就叫做凸多边形。

　　在多边形内部找到一个相对合适的参照坐标点(X, Y)，以该点为中心，分别与多边形各点连接，形成n个独立的三角形，通过上面对点与三角形位置判断的理论，可以分n次判断该点是否在分割的n个独立的三角形内部即可；如下图所示：

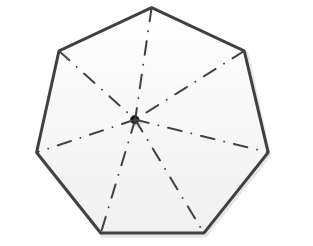
　　找到比较合适的点的方法是：在任意两个内角之间，作这两个内角的角平分线，角平分线的交点的坐标就是我们所要找的参照点。

　　正当我要实现其代码时，在网上发现了一个更加简洁的解决方法，并且，此方法对于多边形没有限制，适用于任意多边形的情况。

思路2：向量叉积法

　　设矢量P = （x1,y1） ，Q = (x2,y2)

　　则矢量叉积定义为：  P × Q = x1*y2 – x2*y1   得到的是一个标量

　　显然有性质 P × Q = – ( Q × P )   P × ( – Q ) = – ( P × Q )

　　如不加说明，下面所有的点都看作矢量，点的乘法看作矢量叉积；

　　叉乘的重要性质：

　　若 P × Q  > 0 ,  则P 在Q的顺时针方向

　　若 P × Q  < 0 ,  则P 在Q的逆时针方向

　　若 P × Q  = 0 ,  则P 与Q共线，但可能同向也可能反向 ，用于判断点是否在边上

　　对于(x0, y0), (x1, y1), ……, (x_{n - 1}, y_{n - 1})这些坐标，若(x_k, y_k)指向(x_{k + 1}, y_{k + 1})的矢量为V_k ，(x_k, y_k)指向(X, Y)的矢量为V_f ，对于所有的k = 0, 1, 2……,n - 1，当k = n - 1时，V_{n- 1} (x_{n - 1}, y_{n - 1})指向(x₀, y₀)

　　1、任意一点(x_k, y_k)使得V_f若为(0, 0)零向量，则点在多边形上；

　　2、若满足V_f在V_k的同一方向（均为逆时针或者顺时针方向），即都满足P × Q  < 0(顺时针为P × Q  > 0)，则点(X, Y)在该多边形内部；

　　3、若不在同一方向且V_f和V_k永远不共线，则在多边形外部；

　　4、若V_f和V_k存在共线情况，则判断使得V_f和V_k共线的点(X, Y)是否在多边形上（V_f  。V_k  >0 且|V_f | < |V_k|则点

(X, Y)在多边形边上），其他则在外部。

　　通过这种方法，很好判断点与任意多边形的位置关系，而且复杂度并不高，C语言代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
//返回1表示内部，0表示边上，-1表示外部
int dotLocation(const double *x, const double *y, int n, const double XG, const double YG)
{
    int currentflag = 0;  //当前状态，根据每次叉乘的值来判断
    int lastflag = 0;  //只在第一次进入循环式赋值，后面依次比较lastflag和currentflag的关系
    int iterN = 0;
    double vectorPX = 0.0, vectorPY = 0.0;
    double vectorQX = 0.0, vectorQY = 0.0;
    double PRODUCT = 0.0;//叉乘
    for(iterN = 0; iterN < n; iterN++)
    {
        vectorPX = XG - x[iterN];
        vectorPY = YG - y[iterN];
        if(vectorPX == 0 && vectorPY == 0) return 0;  //要检测的点若在数组x, y中，表示该点在多边形上
        vectorQX = x[(iterN == n - 1) ? 0 : (iterN + 1)] - x[iterN];
        vectorQY = y[(iterN == n - 1) ? 0 : (iterN + 1)] - y[iterN];
        PRODUCT = vectorPX * vectorQY - vectorQX * vectorPY;//计算叉乘

        currentflag = ( PRODUCT > 0) ? 1 : ((PRODUCT < 0)? -1 : 0);//判断叉乘获取currentflag的值

        if(iterN == 0)//第一次进入循环
        {
            lastflag = currentflag;
        }
        if(currentflag != lastflag)
        {
            switch(currentflag)
            {
            case 0:
                {
                    //叉乘为0时，共线（反向货同向），要分两种情况：1、点在边上；2、点在外部
                    return (vectorPX * vectorQX + vectorPY * vectorQY > 0 && (vectorPX * vectorPX + vectorPY * vectorPY) <= (vectorQX * vectorQX + vectorQY * vectorQY))? 0 : -1;
                }
            default:
                return -1;//点在多边形外部
            }
        }
    }
    return 1;  //点在多边形内部
}
int main()
{
//    double x[3] = { 0.0, 0.0, 1.0 };
//    double y[3] = { 0.0, 1.0, 0.0 };
//    int n = 3;
//    double X , Y;
//    X = 0.5;
//    Y = 0.25;
    double x[4] = { 0.0, 0.0, 1.0, 1.0 };
    double y[4] = { 0.0, 1.0, 1.0, 0.0 };
    int n = 4;
    double X , Y;
    X = 0.6;
    Y = 0.6;
    int result = dotLocation(x, y ,n, X ,Y);
    printf("the result is %d\n", result);
    switch(result)
    {
        case 0: printf("该点在多边形的边上！\n"); break;
        case 1: printf("该点在多边形的内部！\n"); break;
        case -1: printf("该点在多边形的外部！\n"); break;
        default: break;
    }
    return 0;
}