一、打表法
0.http://oeis.org/
1.差分序列:https://blog.csdn.net/wu_tongtong/article/details/79115921
对于一个多项式产生的序列,可以多次求差分序列,直到差分序列均为0,这时原序列的表达式就可以表示为:
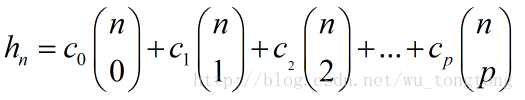
其中,c0……cp为差分表的第0条对角线。
同时有求和公式
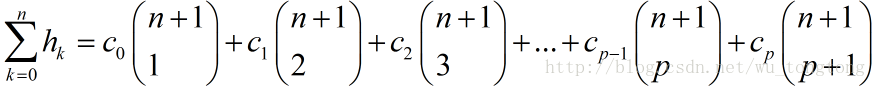
确定有公式后除去可以确定的项

#include <bits/stdc++.h> using namespace std; #define rep(i, a, n) for (ll i=a;i<n;i++) #define SZ(x) ((ll)(x).size()) typedef long long ll; const ll mod = 1000000007; ll powmod(ll a, ll b) { ll res = 1; a %= mod; for (; b; b >>= 1) { if (b & 1)res = res * a % mod; a = a * a % mod; } return res; } ll n; namespace linear_seq { const ll N = 100010; ll res[N], base[N], _c[N], _md[N]; vector<ll> Md; void mul(ll *a, const ll *b, ll k) { rep(i, 0, k + k) _c[i] = 0; rep(i, 0, k) if (a[i]) rep(j, 0, k) _c[i + j] = (_c[i + j] + a[i] * b[j]) % mod; for (ll i = k + k - 1; i >= k; i--) if (_c[i]) rep(j, 0, SZ(Md)) _c[i - k + Md[j]] = (_c[i - k + Md[j]] - _c[i] * _md[Md[j]]) % mod; rep(i, 0, k) a[i] = _c[i]; } ll solve(ll n, vector<ll> a, vector<ll> b) { ll ans = 0, pnt = 0; ll k = SZ(a); rep(i, 0, k) _md[k - 1 - i] = -a[i]; _md[k] = 1; Md.clear(); rep(i, 0, k) if (_md[i] != 0) Md.push_back(i); rep(i, 0, k) res[i] = base[i] = 0; res[0] = 1; while (1ll << pnt <= n) pnt++; for (ll p = pnt; p >= 0; p--) { mul(res, res, k); if (n >> p & 1) { for (ll i = k - 1; i >= 0; i--) res[i + 1] = res[i]; res[0] = 0; rep(j, 0, SZ(Md)) res[Md[j]] = (res[Md[j]] - res[k] * _md[Md[j]]) % mod; } } rep(i, 0, k) ans = (ans + res[i] * b[i]) % mod; if (ans < 0) ans += mod; return ans; } vector<ll> BM(vector<ll> s) { vector<ll> C(1, 1), B(1, 1); ll L = 0, m = 1, b = 1; rep(n, 0, SZ(s)) { ll d = 0; rep(i, 0, L + 1) d = (d + (ll) C[i] * s[n - i]) % mod; if (d == 0) ++m; else if (2 * L <= n) { vector<ll> T = C; ll c = mod - d * powmod(b, mod - 2) % mod; while (SZ(C) < SZ(B) + m) C.push_back(0); rep(i, 0, SZ(B)) C[i + m] = (C[i + m] + c * B[i]) % mod; L = n + 1 - L; B = T; b = d; m = 1; } else { ll c = mod - d * powmod(b, mod - 2) % mod; while (SZ(C) < SZ(B) + m) C.push_back(0); rep(i, 0, SZ(B)) C[i + m] = (C[i + m] + c * B[i]) % mod; ++m; } } return C; } vector<ll> temp; void init(vector<ll> a) { temp = BM(a); temp.erase(temp.begin()); rep(i, 0, SZ(temp))temp[i] = (mod - temp[i]) % mod; } ll gao(vector<ll> a, ll n) { return solve(n, temp, vector<ll>(a.begin(), a.begin() + SZ(temp))); } }; using namespace linear_seq; int main() { vector<ll> v; v.push_back(3); v.push_back(9); v.push_back(20); v.push_back(46); v.push_back(106); v.push_back(244); v.push_back(560); v.push_back(1286); v.push_back(2956); v.push_back(6794); init(v); ll T; scanf("%lld", &T); while (T--) { ll n; scanf("%lld", &n); printf("%lld ", gao(v, n - 1)); } return 0; }
