我们通过将实际问题转化为有向或者无向图来解决最短路最小生成树等问题,那么同样我们也可以建立流网络来解决生活中的其他实际问题,譬如液体在管道中的流动,其它类流体的流动,任务分配,最大流等问题都可以用这种模型解决。
我们可以定义一个流网络G = (V, E)是一个有向图,图中的每一条边(u, v)都有一个非负的容量值c(u, v),我们规定G中不存在一条边的反向边,并且规定如果(u, v)不属于E则c(u, v) = 0,还规定图中不存在自环。我们挑出两个特殊结点源结点s和汇点t,假定图中除这两个结点外的其它结点 v 都存在一条路径满足s - > v - > t。因此流网络是联通的。
我们对该流网络做出其它必要的定义和总结:
容量限制:对于每条边(u, v) ,我们规定f(u, v) <= c(u, v)。( f(u, v)为此边通过的流量)。
流量守恒:对于除s, t外的其它所有结点,要求流入v的流量等于流出v的流量。
反平行边模拟:由于我们假定流网络中不同时存在某条边的反向边,因此我们用一种方法来获得与原图等价的另一个流网络,我们新加入一个结点,让他与存在自环的边形成一个回路,并将他们之间的权值改变为自环对应的权值,这样就生成了一个新的流网络,这个流网络是满足我们假设的。
具有多个源结点和多个汇点的流网络:我们可以新建一个结点作为所有源点的新的源点,新建一个汇点作为所有汇点新的汇点,这样我们就可以将这种问题转换为单个源点和单个汇点的网络流。
最大流:我们定义从源点到汇点的所有流量权和最大的流为最大流。
残留网络:为了求解最大流,我们引入一个新的流网络,名为残留网络。
从直观上看,给定流网络G和流量 f ,残存网络Gf由那些仍有空间对流量进行调整的边构成。流网络的一条边可以允许的额外流量等于该边的容量减去该边的流量。如果该差为正值,则将这条边只与残留网络Gf中,并将其权值设置为Cf(u, v) = C(u, v) - f(u, v)。对于图G中的边来说,只有允许额外流量流入的边才可以加入残存网络。我们也假定如果边(u, v)的流量等于其容量,则Cf(u, v) = 0, 这条边不属于Gf。为了表示对一个正流量的缩减,我们将边(v, u)加入Gf中,并且将其残留网络设置为Cf(v, u) = C(u, v)。
增广路径:增广路径p是残存网络Gf中一条从源结点s到汇点t的简单路径。根据残存网络的定义,对于一条增广路径上的边(u, v),我们可以增加流量的幅度为这条简单路径上权值最小的边对应的权值,这只会使得我们的流量更接近最大流并且不会违反流网络G中对边的限制。
流网络的切割:我们知道可以利用增广路径逐步求出最大流,但是何时我们可以确认我们得到的结果就是最大流呢?我们先引入一个切割的概念,流网络的切割(S, T)为将集合V划分为S 和T = V - S两个集合,并且使得s 属于S, t属于T。
最小割:我们定义一个网络的最小切割是整个网络中容量最小的切割。如何计算一个流网络的切割呢?
如下图,我们可以得出表达式f(v1, v3) + f(v2, v4) - f(v3, v2) = 12 + 11 - 3 = 19。即该切割的净流量为19,该切割的容量为c(v1, v3) + c(v2, v4) = 12 + 14 = 26。
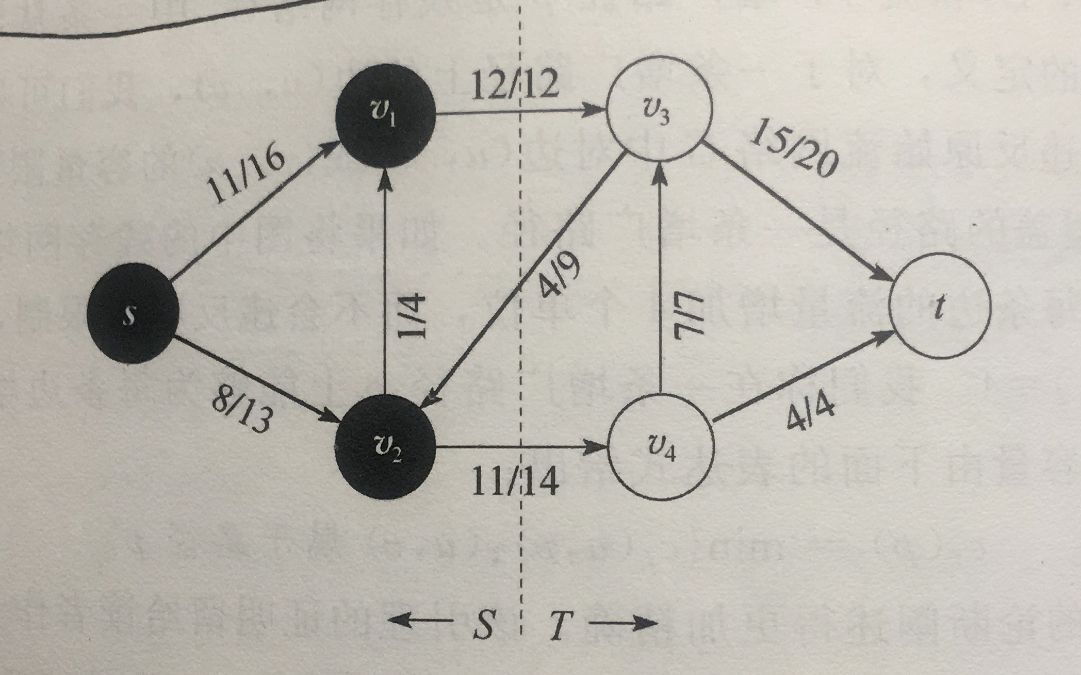
最大流最小切割定理:一个流网络的最大流的值不能超过该网络最小切割的容量值。
下面我们介绍几种算法用于求解最大流:
首先我们介绍一个最为普遍的求解最大流的思路:
Ford-Fulkerson方法:
初始化流每条边的流量 f 为0, 接着在残留网络中寻找一条增广路径对流量进行增广并且更新残留网络,直至残留网络中不存在增广路径则表明当前的值已经是最大值。
伪代码:
1 FORD-FULKERSON-METHOD(G, s, t) 2 Initialize flow f to 0 3 while there exists an augmenting path p in the residual network Gf 4 augment flow f along p //augment and update 5 return f
这是求解最大流的一般思路,求解最大流的算法都是基于该思想给出的。下面我们一 一介绍这些算法:
首先我们给出一个更具体的求解最大流的算法得思路的伪代码:很明显可以看出求解最大流算法的复杂度和第四行求解增广路息息相关。
1 FORD-Fulkerson(G, s, t) 2 for each edge(u, v) 3 (u, v).f = 0 4 while there exists an augmenting path p in the residual network Gf 5 Cf(p) = min(Cf(u, v) : (u, v) is in p) 6 for each edge(u, v) in p 7 if(u, v) belong to E 8 (u, v).f = (u, v).f + Cf(p) 9 else (v, u).f = (v, u) - Cf(p)
Edmonds-Karp算法:
算法思路:该算法在上述思想的基础上在寻找增广路径的操作中使用广度优先搜索来改善其算法的效率。也就是说每次我们选择的增广路是一条从源点s到汇点t的一条最短路径。
参考代码:
1 bool bfs(int s, int t) {//寻找一条从s到t的增广路,若找到返回true,否则返回false 2 int p; 3 queue <int> Q; 4 memset(pre, -1, sizeof pre); 5 memset(vis, false, sizeof vis); 6 pre[s] = s; 7 vis[s] = true; 8 Q.push(s); 9 while(!Q.empty()) { 10 p = Q.front(); 11 Q.pop(); 12 for(int i = 1; i <= n; i ++) { 13 if(r[p][i] > 0 && !vis[i]) { 14 pre[i] = p; 15 vis[i] = true; 16 if(i == t) return true; 17 Q.push(i); 18 } 19 } 20 } 21 return false; 22 } 23 24 int Edmonds_Karp(int s, int t) { 25 int flow = 0, d; 26 while(bfs(s, t)) { 27 d = INF; 28 for(int i = t; i != s; i = pre[i])//寻找路径中权值最小的边进行增广 29 d = d < r[pre[i]][i] ? d : r[pre[i]][i]; 30 for(int i = t; i != s; i = pre[i]) { 31 r[pre[i]][i] -= d;//对每条边在残留网络中的权值进行更新,将最短路上的边的权值减去增加的流d 32 r[i][pre[i]] += d;//对其反向边的容量也进行更新 33 } 34 flow += d; 35 } 36 return flow; 37 }
Dinic算法:
算法思路:该算法就是不停的用BFS构造层次图,然后用阻塞流来增广,层次图即按照图中其它顶点到S的最短步数分层,阻塞流可以看作是不考虑反向弧的极大流。大题步骤就是先构造层次图,接着在层次图中DFS进行寻路
,每次找得到一条路就进行一次增广,接着返回上一个最近的可以继续通过其它路径到达t的顶点,DFS寻路,当发现不存在一条路可以走到t时再对图重新分层,直至分层图中不存增广路径时退出。
这里DFS寻路每次只选择向前走一步能走到的顶点,没有路的就往回退。
1 const int maxn=200+5, INF = 0x3f3f3f3f; 2 3 struct Edge 4 { 5 Edge(){} 6 Edge(int from,int to,int cap,int flow):from(from),to(to),cap(cap),flow(flow){} 7 int from,to,cap,flow; 8 }; 9 10 struct Dinic 11 { 12 int n,m,s,t; //结点数,边数(包括反向弧),源点与汇点编号 13 vector<Edge> edges; //边表 edges[e]和edges[e^1]互为反向弧 14 vector<int> G[maxn]; //邻接表,G[i][j]表示结点i的第j条边在e数组中的序号 15 bool vis[maxn]; //BFS使用,标记一个节点是否被遍历过 16 int d[maxn]; //从起点到i点的距离 17 int cur[maxn]; //当前弧下标 18 19 void init(int n,int s,int t) 20 { 21 this->n=n,this->s=s,this->t=t; 22 for(int i=1;i<=n;i++) G[i].clear(); 23 edges.clear(); 24 } 25 26 void AddEdge(int from,int to,int cap) 27 { 28 edges.push_back( Edge(from,to,cap,0) ); 29 edges.push_back( Edge(to,from,0,0) ); 30 m = edges.size(); 31 G[from].push_back(m-2); 32 G[to].push_back(m-1); 33 } 34 35 bool BFS() 36 { 37 memset(vis,false,sizeof(vis)); 38 queue<int> Q;//用来保存节点编号的 39 Q.push(s); 40 d[s]=0; 41 vis[s]=true; 42 while(!Q.empty()) 43 { 44 int x=Q.front(); Q.pop(); 45 for(int i=0; i<G[x].size(); i++) 46 { 47 Edge& e=edges[G[x][i]]; 48 if(!vis[e.to] && e.cap>e.flow) 49 { 50 vis[e.to]=true; 51 d[e.to] = d[x]+1; 52 Q.push(e.to); 53 } 54 } 55 } 56 return vis[t]; 57 } 58 59 int DFS(int x,int a) 60 { 61 if(x==t || a==0)return a; 62 int flow=0,f;//flow用来记录从x到t的最小残量 63 for(int& i=cur[x]; i<G[x].size(); i++) 64 { 65 Edge& e=edges[G[x][i]]; 66 if(d[x]+1==d[e.to] && (f=DFS( e.to,min(a,e.cap-e.flow) ) )>0 ) 67 { 68 e.flow +=f; 69 edges[G[x][i]^1].flow -=f; 70 flow += f; 71 a -= f; 72 if(a==0) break; 73 } 74 } 75 return flow; 76 } 77 78 int Maxflow() 79 { 80 int flow=0; 81 while(BFS()) 82 { 83 memset(cur,0,sizeof(cur)); 84 flow += DFS(s,INF); 85 } 86 return flow; 87 } 88 }Dinic;