1.对某些线性回归问题，正规方程给出了更好的解决方法，来求得参数θ，截止到目前我们一直使用线性回归算法是梯度下降法，为了最小化代价函数J(θ)，我们使用梯度下降多次迭代，来收敛得到全局的最小值。与此相反的正规方程提供了一种求θ的解析方法，我们不需要再去运用迭代的方法，而是可以直接一次性的求解θ最优值。只需要一步就可以求得最小值
(1)例1：假设有个简单的代价函数J(θ)，它是实数θ的函数，所以现在假设θ是一个标量或者θ是一个实数值，只是一个数字，不是矢量
，假设代价函数J是这个实参数θ的二次函数，所以J(θ)看起来是这样的：
怎么最小化一个二次函数呢？如果你了解微积分，你知道最小化一个函数的方法就是对它进行求导，并且将导数置为0，所以对J求关于θ的导数，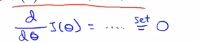 
，然后直接将导数置为0，这样就可以求得使得J(θ)最小的θ值，这是θ为实数的一个比较简单额例子。在机器学习问题中，θ不是一个实数，而是一个n+1维的参数向量，而代价函数J(θ)是向量(即θ0到θm的函数)，这个代价函数看起来就是这样的。
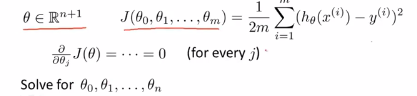
那怎么最小化代价函数J呢？微积分告诉我们，逐级的对参数θ_j求J的偏导数，然后将他们全部置为0，如果这样做并且求出θ0到θn的值，这样就能得到最小化代价函数θ的值 ，如果真的做完微积分， 并且求出θ0到θn，这个偏微分最终可能很复杂。接下来要做的不是遍历所有的偏微分，因为这个太费事了。 我们要做的是使得代价函数J(θ)最小化的θ值。
(2)example:m=4
假设我们有4个训练样本m=4，为了实现正规方程的方法，假设这四个训练集就是我们所有的数据，我们需要做的是在数据集中加上一列，对应额外特征变量的x0，它的取值永远是1：
接下来需要做的是构建一个矩阵X，这个矩阵包含了训练样本所有的特种额变量，具体来说下图中绿色框框就是我们特征变量，我们要把这些数字全部放进矩阵中X去，只是赋值每一列数据到下面的矩阵中去
我们对y值进行类似的操作，我们将预测值构建一个向量，如下图所示：
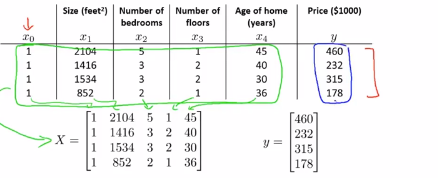
并称之为向量y，所以X是一个m x (n+1)维的矩阵，y是一个m维的向量，其中m是训练样本数量，n是特征变量数，其实是n+1列，因为我们在前面加上了这个额外的特张变量x0。最终如果用矩阵X和向量y来计算θ，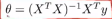
，这样就能够求得使代价函数最小化的θ值，
(3)m个样本，n个特征向量：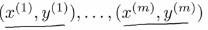
，所以得到的每一个训练样本xi，都可能是n+1维的特征向量：
构建矩阵X的方法，也被称为设计矩阵，如下图所示，每个训练样本给出这样的特征向量，比如这里的n+1维向量，构建设计矩阵的方法，就是构建这样的矩阵，我们要做的是取第一个训练样本，也就是一个向量，取出它的转置，最后长成的样子是这样扁长的样子，来作为矩阵的第一行，然后将第二个样本进行转置加进来，把它作为第二行以此类推，直到最后一个样本，取出其转置，并将其作为X矩阵的最后一行，这就是矩阵X，是一个m*(n+1)维的矩阵。举出一个简单的例子，加入我们只有一个特征变量，除了x0之外只有一个特征变量，