概率笔记1——独立事件下的简单概率

基础概率和简单概率

硬币和骰子

　　一个硬币有两面，我们都知道，投掷一次硬币，正面朝上的概率是50%；一个骰子有六个数字，投掷一次骰子，每个数字出现的概率均等，都是1/6

　　上述两个概率用数学解释就是：一个事件的概率 = 满足要求的事件数目 / 所有等可能性事件的数目。所以硬币正面朝上的概率 P(head) = 1/2，数字1在骰子中出现的概率是P(1) = 1/6。

　　同样的，因为一个骰子有3个偶数，抛掷一次骰子，偶数出现的概率就是P(偶数) = 3/6 = 1/2；因为没有任何一面有两个数字，所以同时出现2或3的概率是 P(2 or 3) = 0/6 = 0

不同颜色的弹珠

　　袋子里装有8个弹珠，其中3个黄色，2个红色，2个绿色，1个蓝色。从袋子里拿出一个弹珠，弹珠是黄色概率？

　　如上图所示，很容易得知P(yellow) = 3/8

概率相加

　　将一副扑克牌去掉大小王，剩余的52张牌中共四种花色，每种花色13张，很容易知道抽到J的概率是 P(J) = 4/52 = 1/13；抽到♠的概率P(♠) = 13/52 = 1/4；抽到♠J的概率 P(♠J) =  1/52；抽到J或♠的概率是多少呢？

　　先看下图：

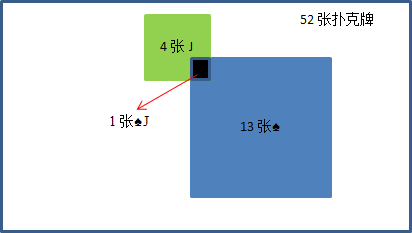
　　J或♠的概率就是绿色和蓝色正方形所覆盖的面积，P(J or ♠) = (4 + 13 - 1)/52 = 4/13

　　由于重叠部分是P(J and ♠)，故P(J or ♠) = P(J) + P(♠) - P(J and ♠) = 4/52 + 13/52 – 1/52 = 4/13，由此得到概率相加公式：

P(A or B) = P(A) + P(B) – P(A and B)

　　将or和and用集合符号表示：

P(A∪B) = P(A) + P(B) – P(A∩B)

　　其中P(A∩B)可简写作P(AB).

　　如果P(A and B) = 0，则A和B是互斥事件，P(A)和P(B)是互斥概率。

独立事件的组合概率

等概率事件

　　计算一枚硬币两次投掷出正面的概率。

　　如果H表示正面，T表示方面，两次投掷的所有可能是：HH, HT, TH, TT，所以P(HH) = 1/4

　　在投掷时，第一次投掷的结果对第二次投掷没有任何影响，我们称这两次投掷事件是相互独立的。对于独立事件，过去事件发生的概率不影响将来事件的概率。

　　对于本例，两次投掷出正面的概率 = 第一次投出正面的概率×第二次投出正面的概率，即P(HH) = P(H₁)·P(H₂) = 1/2 × 1/2 = 1/4。同理，如果有三枚硬币，P(THT) = P(T₁)P(H₂)P(T₃) = 1/8

　　当A₁A₂A₃……A_n相互独立，

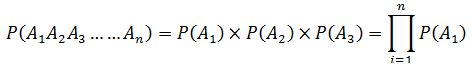
不等概率事件

　　假设硬币是不均匀的，每次投掷硬币后正面朝上的几率更大，P(H) = 60%，投掷一次硬币就是一个不等概率事件。很容易得知 P(T) = 1 – P(H) = 40%

　　连续投掷两次硬币，正面朝上的概率：

P(H₁H₂) = P(H₁)·P(H₂) = 60% × 60% = 36%

　　连续投掷三次硬币，两次正面一次反面订单概率：

P(H₁H₂ T₃) = P(H₁)·P(H₂)·P(T₃) = 60% × 60% × 40% = 9.6%

　　可以看出，在独立事件样本中，等概率和不等概率事件并没有差别。

示例

示例1

　　有一个周长是36π的圆，圆中又包含了一个面积是16π的小圆，现在大圆中随机选择一点，该点落在小圆中的概率？

　　S_bigCircle = π(36/2)² = 324π,  P(point also in smaller circle) = 16π/  324π = 4/81

示例2

　　某机构举行了一次抽奖活动，一共有两个奖品，当第一个奖券被抽到后，把奖券贴到奖品上，再抽第二个奖券决定获奖者。这两次个抽奖事件是相互独立的事件吗？

　　不是。独立事件的含义是一个事件的结果不影响其它事件的结果。本例中两个事件是有关联的，因为奖券的数目是固定的，第一张奖券贴好后，奖券总数将减少一张，第二张奖券将不可能是第一张奖券。可以想象一下有三张分别标有A、B、C的奖券，第一次A被抽到，第二次抽到的只可能是B或C，所以第二个事件的结果和第一次抽到的奖券是相关的，两个事件不是相互独立的。使它们互相独立的方法是，每次抽到奖券后写上获奖者的名字，再将奖券放入奖券箱重新参与抽奖，而不是贴到奖品上。

示例3

　　有两道选择题，第一题有四个答案，第二题有三个答案，每道题只有一个答案是正确的。如果使用随机猜测法，猜对每个问题的概率是多少？同时猜对两个问题的概率是多少？

　　P(test1) = 1/4,  P(test2) = 1/3

　　P(test1 and test2) = P(test1 ∩ test2) = P(test1) × P(test2) = 1/12

　　假设两题的正确选项分别是D和B，本例可以用下面的表格描述：

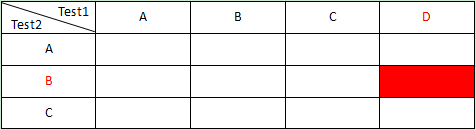
　　共有12个方格，红色方格是两个问题都猜对的概率。所以说概率就是面积。

示例4

　　投三次骰子，均投得偶数的概率？骰子是六面体。

　　三次事件是相互独立的，每次投出偶数的概率是3/6，三次均投出偶数的概率：

　　P = (3/6) × (3/6) × (3/6) = 1/8

　　几率很小啊，并不是赌徒们认为的1/2，所以十赌九输啊。

示例5

　　投掷三枚硬币，

1. 恰好两枚正面朝上的概率？
2. 至少有一次正面朝上的概率？

　　可以列出所有可能的结果：HHH, HHT, HTT, HTH, THH, THT, TTH, TTT。由此可知问题1的答案P(Exactly 2 H) = 3/8；问题2的答案P(at least 1 H) = 7/8

　　如果投掷更多的硬币，画图法就不靠谱了，必须找到数学方法。先来看样本空间的样本数量，每次投掷硬币可以得到两种结果，投掷3次，根据乘法结合律可以得到2×2×2种结果。再来看满足要求的事件数目，对于问题1，可以看作共有三个位置，其中恰好有两个安插了正面朝上的硬币，它们的顺序无关紧要，这是典型的组合问题，可以用  表示。于是问题1变成了：

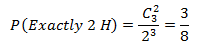
　　对于问题2，相当于1减所有反面朝上的概率：

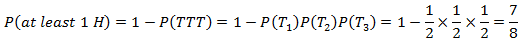
　　如果投掷10次硬币：

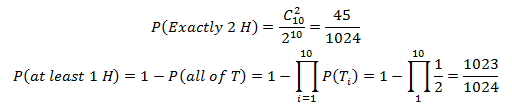
在n个独立事件中发生k个事件的概率

　　将上面的示例5扩展，投掷n个硬币，恰好有k个正面朝上：

---

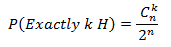
 　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！