[Codeforces 1201D]Treasure Hunting(DP)

[Codeforces 1201D]Treasure Hunting(DP)

题面

有一个n*m的方格，方格上有k个宝藏，一个人从(1,1)出发，可以向左或者向右走，但不能向下走。给出q个列，在这些列上可以向上走，其他列不能向上走。可以重复经过同一个点。求从(1,1)出发，经过所有宝藏的最短路径长度

(n,m,k,q leq 2 imes 10^5)

分析

贪心考虑，我们应该按照行一层一层的走。每一行应该从最左的宝藏走到最右的宝藏，或者从最右的宝藏走到最左的宝藏，然后找最近的一个可以向上走的列，走到另一行。

设(dp[i][0/1])表示当前在第i行最左边的宝藏，或者最右边的宝藏，已经走完该行所有宝藏的最短距离

那么只要记录上一个有宝藏的行pre,分类讨论一下四种转移

(dp[i][0])需要先走到第i行的最右端，再从第i行的最右端走到最左端

(dp[i][1])需要先走到第i行的最右端，再从第i行的最右端走到最左端

另一个问题是如何计算(x1,y1)到(x2,y2)的距离。我们预处理在第i列左边最近的可以向上走的列lb[i],和最右边最近的列rb[i],那么我们走的列一定是lb[y1],lb[y2],rb[y1],rb[y2]四列中的一列。

如下图，假设y1<y2,走lb[y1]左侧的一列显然不如lb[y1]优，走rb[y2]右侧的一列显然不如rb[y2]优，而走rb[y1],lb[y2]中间的列和直接走rb[y1],lb[y2]一样

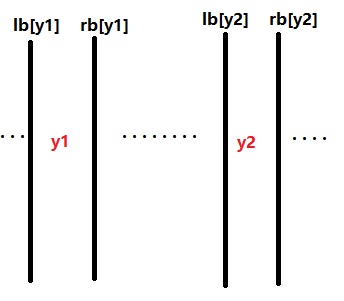
把经过这四列向上的距离统计出来就可以了

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define maxn 200000 
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
int n,m,k,q;
vector<int>a[maxn+5];
int lb[maxn+5],rb[maxn+5];
int col[maxn+5]; 
ll dp[maxn+5][2];//走到最左侧/最右侧结束 
ll calc(int y1,int y2,int line){//从y1到第line列，走上去，再到y2
	return (ll)abs(y1-line)+abs(y2-line);
}
ll dist(int x1,int y1,int x2,int y2){
	ll distx=abs(x1-x2);
	ll disty=min(min(calc(y1,y2,lb[y1]),calc(y1,y2,lb[y2])),min(calc(y1,y2,rb[y1]),calc(y1,y2,rb[y2])));
	return distx+disty;
}
int main(){
	int x,y;
	scanf("%d %d %d %d",&n,&m,&k,&q);
	for(int i=1;i<=k;i++){
		scanf("%d %d",&x,&y);
		a[x].push_back(y); 
	}
	for(int i=1;i<=q;i++){
		scanf("%d",&col[i]);
	}
	sort(col+1,col+1+q);
	col[0]=-INF;
	col[q+1]=INF;
	for(int i=1;i<=m;i++){
		lb[i]=col[lower_bound(col+1,col+1+q,i)-col-1];
		rb[i]=col[lower_bound(col+1,col+1+q,i)-col];
	} 
	
	sort(a[1].begin(),a[1].end());
	if(!a[1].empty()){
		dp[1][0]=dp[1][1]=a[1].back()-1;
		a[1][0]=a[1].back();
		//第一行必须从最后一个关键点往上走，否则就走不完所有关键点 
	}else{
		a[1].push_back(1);
		dp[1][0]=dp[1][1]=0;
	}
	int last=1;
	for(int i=2;i<=n;i++){
		if(!a[i].empty()){
			sort(a[i].begin(),a[i].end());
			ll l_to_l=dp[last][0]+dist(last,a[last].front(),i,a[i].front());//从pre行最左侧走到i行最左侧
			ll r_to_l=dp[last][1]+dist(last,a[last].back(),i,a[i].front()); //从pre行最右侧走到i行最左侧
			ll l_to_r=dp[last][0]+dist(last,a[last].front(),i,a[i].back());//从pre行最左侧走到i行最右侧
			ll r_to_r=dp[last][1]+dist(last,a[last].back(),i,a[i].back());//从pre行最右侧走到i行最右侧
			ll now=a[i].back()-a[i].front();//走完当前行的代价 
			dp[i][0]=min(l_to_r,r_to_r)+now;//先走到最右侧，最后到最左侧 
			dp[i][1]=min(l_to_l,r_to_l)+now;//先走到最左侧，最后到最右侧 
			last=i;
		}
	} 
	printf("%I64d
",min(dp[last][0],dp[last][1]));
	
}