Coder
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2778 Accepted Submission(s): 1104
Problem Description
In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write
an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done. 1
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
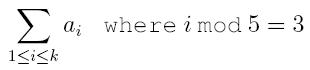
where the set S is written as {a1, a2, ... , ak} satisfying a1 < a2 < a3 < ... < ak
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
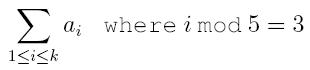
where the set S is written as {a1, a2, ... , ak} satisfying a1 < a2 < a3 < ... < ak
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
Input
There’re several test cases.
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
Output
For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.
Sample Input
9 add 1 add 2 add 3 add 4 add 5 sum add 6 del 3 sum 6 add 1 add 3 add 5 add 7 add 9 sum
Sample Output
3 4 5HintC++ maybe run faster than G++ in this problem.解题思路:建5棵线段树。分别保存区间内相对顺序模5的位置的数字之和。pushup的时候左子树的相对父节点位置不变。右子树的相对位置为((i-tree[[rt<<1].cnt])%5+5)%5,cnt是区间内的数的个数,最后结果是tree[1].sum[3]#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <string> #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define Maxn 100005 #define LL long long using namespace std; struct { int cnt; LL sum[5]; }tree[Maxn<<2]; void push_up(int rt) { for(int i=0;i<5;i++) tree[rt].sum[i]=tree[rt<<1].sum[i]+tree[rt<<1|1].sum[((i-tree[rt<<1].cnt)%5+5)%5]; } void build(int l,int r,int rt) { tree[rt].cnt=0; memset(tree[rt].sum,0,sizeof(tree[rt].sum)); if(l==r) return ; int m=(l+r)>>1; build(lson); build(rson); push_up(rt); } void update(int pos,int x,int k,int l,int r,int rt) { tree[rt].cnt+=k; if(l==r) { tree[rt].sum[1]+=k*x; return ; } int m=(l+r)>>1; if(pos<=m) update(pos,x,k,lson); else update(pos,x,k,rson); push_up(rt); } int main() { char op[Maxn][5]; int x[Maxn],n,num[Maxn],j,p; freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); while(~scanf("%d",&n)) { j=0; for(int i=0;i<n;i++) { scanf("%s",op[i]); if(op[i][0]!='s') { scanf("%d",&x[i]); if(op[i][0]=='a') num[j++]=x[i]; } } sort(num,num+j); if(j==0) memset(tree[1].sum,0,sizeof(tree[1].sum)); else build(1,j,1); for(int i=0;i<n;i++) { switch(op[i][0]) { case 'a': p=lower_bound(num,num+j,x[i])-num+1; update(p,x[i],1,1,j,1); break; case 'd': p=lower_bound(num,num+j,x[i])-num+1; update(p,x[i],-1,1,j,1); break; case 's': printf("%I64d ",tree[1].sum[3]); break; } } } return 0; }
Source