Codeforces Round #635 (Div. 1)（A）

A. Linova and Kingdom

题意：题目给你n个点，n-1条边，其中1号节点为根，从中国选出k个点为工业城市，其余的点为旅游城市，工业城市会派一个人到1号城市去，问，所有人经历的所有的旅游城市的人数为多少？

题解：这个题目要求所有的旅游城市数量的最大值，很简单党的我们可以看出来，一定要选择距离根节点的最远的叶子，我们以下面的这张图片为例子进行讨论：

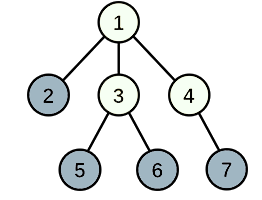
我们在确定工业城市的时候，选择5，6，7很容易理解，但为什么不选择3or4作为工业城市呢，是因为选择2，3，4的影响都是一样的吗？答案显然不是。我们选择2的时候，ans=1+2+2+2；选择4的时候，ans=2+2+1+1。我们可以看出来，当一个节点有子节点的时候，若我们选择该节点为工业城市，会使它的子节点的单个贡献值分别减一，而根据贪心策略，当我们选择某个节点为工业城市的时候，那它的子节点也一定被选定为哦那个也城市了（如果有存在），这样，我们可以得到如下关系：

　　单个节点的贡献值=该节点距离根节点的距离-该节点的子节点个数

那么，我们就可以将所有节点的贡献值算出来，按降序排序在取即可。

代码：

#include<iostream>
#include<vector>
#include<algorithm>
#define ll long long
using namespace std;
vector<int> G[200005];
ll sz[200005]={0};//存储相应节点的子节点的个数 
ll an[2400005]={0};
void dfs(ll v,ll p,ll d){
    sz[v]=1;
    for(ll i=0;i<G[v].size();i++){
        ll u=G[v][i];
        if(u==p){
            continue;
        }
        dfs(u,v,d+1);
        sz[v]=sz[v]+sz[u];
    }
    an[v]=d-sz[v];
}
bool cmp(ll a,ll b){
    return a>b;
}
int main(){
    ll n,m;
    cin>>n>>m;
    ll u,v;
    for(ll i=1;i<n;i++){
        cin>>u>>v;
        G[u].push_back(v);
        G[v].push_back(u);
    }//数据输入完毕，下面开始处理
    dfs(1,1,1);
    sort(an+1,an+1+n,cmp);
    ll sum=0;
    for(ll i=1;i<=m;i++){
        sum=sum+an[i];
    }
    cout<<sum<<endl;
    return 0;
}