又到节假日,园子里面不少高人再次对12306网站的各种问题的各种分析和提出各种解决方案,我也看了这些讨论文章,出于也是一个买票难的“码农”,也来献计献言,把我跟其他人讨论的结果汇总发表一下,希望抛砖引玉,解决铁道部火车票的数据查询和存储问题。
现在,12306网站给人的第一感受就是购票过程网页很卡,不少人分析是由于数据库非常庞大,有复杂的查询和数据传输,并着重在数据库的设计方面大作文章,却很少有人在数据存储“量”上下功夫。或许大家都说现在磁盘那么便宜,还要刻意关注数据存储量的大小么?我觉得做一个大型的系统必须关注这个问题,因为数据量决定了数据的存储方式、查询方式、处理方式等等,比如数据量太大了一般就要分表甚至分库,甚至分数据中心,数据量大了处理不过来就需要数据库做集群,还有灾备方案等等,甚至,数据量大了,还得在业务处理上做出改变,比如把过期的数据放到备用库去,当前系统只用最常用的数据。
12306的数据肯定有很多种,这里我只讨论“车票数据”,
它涉及的数据有:
- 车票数量、
- 余票数量、
- 座位号、
- 车厢号、
- 车次、
- 站次、
- 发车时间等;
(同样,为简化设计,我们这里假设车票都是从起点到终点的,没有考虑到中间的站到站的票。)
涉及的业务操作有:
- 查询是否有票、
- 查询余票数量、
- 查询座位信息(是否有空位、空位位置)、
- 更新座位信息(买票、退票);
车票数据该如何存储呢?我跟有的朋友交流,他们说至少要设计这样的数据表:
----------------------------------------
车票表:
========================
int 唯一标识 NOT NULL,
----------------------------------------
int 车次号 NOT NULL,
----------------------------------------
datetime 发车时间 NOT NULL,
----------------------------------------
int 车厢号 NOT NULL,
----------------------------------------
int 座位号 NOT NULL
----------------------------------------
计算下,这个表存储一行数据需要 4+4+8+4+4=24个字节
假设一列车中的每一节车厢,最多有128个座位(实际上没有这么多,卧铺车厢座位更少)
那么1节车厢的座位占据的数据量是 128 * 24=3072字节
假设每列火车有20节车厢,那么车票数据共需要占用 3072 * 20=61440 字节
至于全国每年会发多少趟车,一共会卖出多少张车票,由于没有准确数字,我这里就不计算了,但相信肯定是一个很大的数字,13亿人每个人每年平均都坐过一次火车吧?那么这个火车票数量还是很庞大的。
说了车票数量,我们来说说旅客买到一张票,他对一列火车中车票数据的查询情况:
对1个人而言,最低需要查询1次,最多需要查询128 * 20=2560 次,每人平均查询量= 1280次;
对整个列车的人而言,买完所有的票,需要查询 1280次 * (128座位 * 20节车厢) = 3276800 次(好熟悉的数字)
-------------------------------
使用数据库表的方式来存储车票数据,我们卖出所有的一趟车的车票,居然有高达300多万次查询!
而且,在国庆、春运等客流量高峰时段,这些查询次数还会更大、更密集!
分析到了这里,我们似乎已经发现了,12360的车票购买系统,最大的瓶颈,不仅仅在于数据量,还包括查询次数和查询频度!
问题找到了,我们就来看看如何降低数据量,降低查询次数,来作为系统优化的关键点。
颠覆传统的设计方案--“二进制位”车票数据查询与存储方案
关键思想,就是利用二进制中的 0,1 来表示座位情况,即:
如果当前位等于0,表示空位,可以售票,如果等于1,表示无空位,票已经售出。
所以,一张车票,仅需一个二进制位!
假设一列车有20节车厢,每节车厢128个座位,那么仅需要 20 * (128/8)=320 字节来存储整列火车的车票信息。
各位看官,如果有板凳、西红柿等等的,请先别乱扔,且听下文分解:)
(注意:
为讲述方便,下面会借用一些计算机语言中的某些概念,如变量申明、位操作等,但仅作为“伪代码”使用,不跟某个具体的语言相对应。)
一、方案设计
1,如何卖票?
假设有一个字节表示1-8号位置,卖票的时候,只需要将字节中指定位置的“位”置为1即可。
那么我们定义一个字节变量:
byte P=0x00;
卖出第一张票,那么现在的座位情况是“0000 0001” ,变量变为 P=0x01;
卖出第二张票,那么现在的座位情况是“0000 0011” ,变量变为 P=0x03;
卖出第三张票,那么现在的座位情况是“0000 0111” ,变量变为 P=0x07;
卖出第四张票,那么现在的座位情况是“0000 1111” ,变量变为 P=0x0F;
卖出第五张票,那么现在的座位情况是“0001 1111” ,变量变为 P=0x1F;
卖出第六张票,那么现在的座位情况是“0011 1111” ,变量变为 P=0x3F;
卖出第七张票,那么现在的座位情况是“0111 1111” ,变量变为 P=0x7F;
卖出第七张票,那么现在的座位情况是“0111 1111” ,变量变为 P=0xFF;
2,如何标记车票已经卖出?
现在的问题是,卖出一张票的时候,怎么将变量指定位置的数置为1?
其实,可以对位进行“OR”操作,
例如当卖出第五张票的时候,可以这样执行:
P5= 0x0F OR 0x10 = 0x1F
其中,0x10 就是 “0001 0000”
同理,
例如当卖出第六张票的时候,可以这样执行:
P6= 0x1F OR 0x20 = 0x3F
... ...
3,如何查询有空位?
假设我们这个变量P是严格保护的,没有外在因素作用于它,那么很简单,当 P<>0xFF ,那么肯定还有座位。
4,如何查询特定位置是否还有空位(有票)?
现在大部分车都需要买票的时候挑选座位,假设以后某列车很特别,需要挑选座位的功能,我们也可以简单实现:
例如,查询2号位置是否有座:
假设2号位置有座,那么我们可以这样表示(假设其它位置都有人在坐):P=“1111 1101”,那么进行下面的运算:
P XOR 0x02 = "0000 0000" = 0
假设2号位置无座,那么我们可以这样表示(假设其它位置都有人在坐):P=“1111 1111”,那么进行下面的运算:
P XOR 0x02 = "0000 0000" = 1
同理,要查询3号位置是否有座,那么只需要
P XOR 0x4
即可,如果结果=1,表示无座,可以卖出一张票,反之,则当前位置不可以卖出车票。
5,如何计算座位号?
我们规定,在一列车厢里面,有 8 * N 个座位,那么我们用一个数组来存储该列车厢中所有的座位:
byte[] B=byte[N];
显然,1-8号位置,是 B[0],9-16号,是B[1]... 以此类推,便可计算出所有的所有的座位号了。
6,如何退票
退票,就是将制定座位号的数的特定位置重新置回二进制位的“0”,具体过程,相信看了前面的说明,不用我再说了吧?
二、方案比较
1,查询某趟车是否还有空位,需要查询多少次?
假设一列火车的座位数据为 byte[] T = byte[320], 那么只需要取 T[n]<>0xFF (n>=1,n<=320),最多总共只需要执行 320 次查询,平均算160次;
对整个列车的人而言,买完所有的票,需要查询 160次 * (128座位 * 20节车厢) = 409600 次,
当前方案的查询次数是传统查询方案的 1/8 。
2,查询某趟车是否还有空位,查询的数据量是多少?
假设对某次列车的全部火车票的数据进行遍历,那么查询处理的数据量仅为 320字节!
那么查询所需要的IO吞吐量,将是原有方案的 320 / 61440 = 1 /192 。
3,查询某趟车是否还有空位,查询效率提升了多少?
假设效率 E 跟查询次数 C 和数据量D成某个函数关系 E=C * D ,那么原有方案的效率比当前方案的效率相当于 1/ 1280
看到了吗?现有方案,在查询效率上,有“数量级”的性能提升,是原有方案的1536倍!
4,其它操作的效率?
查询指定位置的车票是否已经买车、将指定座位号的车票卖出或者退票,这些都需要遍历整个车的车票数据,带来查询次数和查询的数据量问题,其实这个效率影响跟第3个问题应该差不多,也会有“数量级”的性能提升,具体的效率就由大家去计算了。
三、方案的并发与效率问题
本文发出后,下面回复的朋友一致指出了“锁”的问题,因为在传统的高并发程序中,“锁”似乎是必不可少的,必须用锁来保证数据的一致性。所以,这里补充一节内容进行说明。
另外,我还需要特别说明的是,我的方案不是一个数据库里面的数据存储与查询方案,这是一个完全基于内存数据计算的方案,因为它的数据量足够小,全部的车票数据放到内存中也是没有问题的。
1,不需要锁的“并发”方案
当有一个线程准备进行对车票锁定的时候(在火车售票过程中,只要查询到有票就会锁定该票,以便顺利完成下面的售票过程),实质上是将当前查询到的字节中指定的位置置为“1”,出票的时候是确认该操作,而放弃购票的话将该位置重新置为“0”即可。
那么如何标记当前位置(字节)有线程正在使用呢?
假设当前位置的序号是S,数据是P,如果它正被前面一个线程使用,那么它必定某个位置已经被置为了“1”,假设P当前的情况是 "0000 0011" , 那么肯定 P〉0 ,于是新的序号S=S+1,第二个线程使用的数据为P2。
但这里还有一个问题,前面的这个数据P还有空位没有被填充使用完,所以,我们可以规定数据P一直被它原来使用的线程持有,直到填满,P=0xFF 为止。
由此,我们推导出第二个重要的方案
2,批量“写入”方案
由于数据P一直被它原来使用的线程持有,所以这个线程完全可以等待下一个购票人来使用。注意这里的区别,是等待另外一个人,而不是另外一个线程来争抢。于是,我们便完成了批量写入购票信息的方案。写入之后,该线程再释放,获得另外一个新的数据序号S,进行新的处理。注意,这里的序号S其实是我们车厢车票数组的下标,它本身是不需要进行锁定然后加一的,它仅仅是一个存放在“寄存器”的循环变量。
3,内存数据高效加载技术
CPU取数据最快的地方是L1 Cache,通常计算机它的大小是 64字节,我们惊奇的发现,我们一节车厢的128个字节,仅需要加载2次就可以处理完,如果我们的CPU有2个核,那么我们的每个CPU可以同时分别加载64个字节,然后分别进行计算处理。
如果采用1个CPU只运行1个线程的处理方案,128字节的车票数据分别在2个物理线程(CPU核)中处理,这2个线程根本无需考虑锁的问题。
该理论可能令很多人难以理解,因为它涉及了真正的物理上的计算机知识,这里不做更多说明,详细内容,请参看著名的LMAX开源高性能架构Disruptor的
Disruptor 全解析(6):为什么它这么快 (二) - 神奇的 cacheline 补齐
实际上,这里的第1点和第2点,原理也比较类似Disruptor的RingBuffer技术,详细内容可以参考
Disruptor 全解析(6):为什么它这么快 (二) - 神奇的 cacheline 补齐
四、方案总结与设想
通过前面的分析,我们发现采用二进制位进行车票数据的查询和存储,能够极大地提升整个系统的操作效率,降低存储量,降低查询次数,而这正是现在12306最需要优化的关键点。
由于该方案精巧的设计,使得整个12306网站不必依赖于庞大的存储设备和计算设备,以现在服务器的本身配置的超大内存和磁盘存储空间以及CPU计算能力,运行该方案应该很轻松。如果再使用 Disruptor 这样的架构(号称每秒处理600万订单),那么12306网站的问题,是有可能得到解决的。下面是它的架构图:
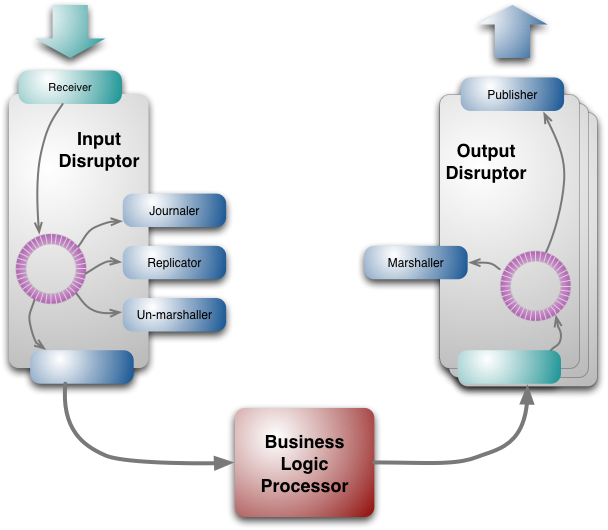
附录:
The LMAX Architecture