交替最小二乘ALS

https://www.cnblogs.com/hxsyl/p/5032691.html

http://www.cnblogs.com/skyEva/p/5570098.html

1. 基础回顾

矩阵的奇异值分解 SVD

（特别详细的总结，参考 http://blog.csdn.net/wangzhiqing3/article/details/7446444）

• 矩阵与向量相乘的结果与特征值，特征向量有关。
• 数值小的特征值对矩阵-向量相乘的结果贡献小

1）低秩近似

2）特征降维

相似度和距离度量

（参考 http://blog.sina.com.cn/s/blog_62b83291010127bf.html）

2. ALS 交替最小二乘（alternating least squares）

在机器学习中，ALS 指使用交替最小二乘求解的一个协同推荐算法。

• 它通过观察到的所有用户给商品的打分，来推断每个用户的喜好并向用户推荐适合的商品。

     

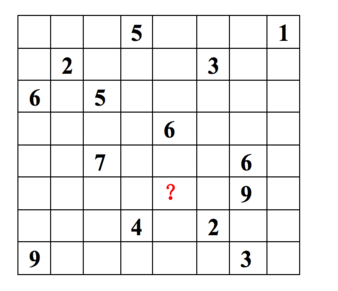
每一行代表一个用户（u1,u2,…,u8）, 每一列代表一个商品（v1,v2,…,v8）,用户的打分为1-9分。

这个矩阵只显示了观察到的打分，我们需要推测没有观察到的打分。

• ALS的核心就是这样一个假设：打分矩阵是近似低秩的。

换句话说，就是一个m*n的打分矩阵可以由分解的两个小矩阵U（m*k）和V（k*n）的乘积来近似，即 A=UV^T,k<=m,n 。这就是ALS的矩阵分解方法。

这样我们把系统的自由度从O(mn)降到了O((m+n)k)。

• 低维空间的选取。

这个低维空间要能够很好的区分事物，那么就需要一个明确的可量化目标，这就是重构误差。

在ALS中我们使用 F范数 来量化重构误差，就是每个元素重构误差的平方和。这里存在一个问题，我们只观察到部分打分，A中的大量未知元是我们想推断的，所以这个重构误差是包含未知数的。

解决方案很简单：只计算已知打分的重构误差。

     

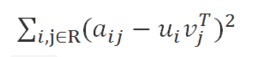
 3. 协同过滤

协同过滤分析用户以及用户相关的产品的相关性，用以识别新的用户-产品相关性。

协同过滤系统需要的唯一信息是用户过去的行为信息，比如对产品的评价信息。

• 推荐系统依赖不同类型的输入数据，最方便的是高质量的显式反馈数据，它们包含用户对感兴趣商品明确的评价。例如，Netflix收集的用户对电影评价的星星等级数据。
• 但是显式反馈数据不一定总是找得到，因此推荐系统可以从更丰富的隐式反馈信息中推测用户的偏好。 隐式反馈类型包括购买历史、浏览历史、搜索模式甚至鼠标动作。

4. 显示反馈模型

通过内积 r_ij = u_i^T v_j 来预测，另外加入正则化参数 lamda 来预防 过拟合。

最小化重构误差：

 

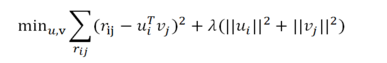
5. 隐式反馈模型

偏好：二元变量 ，它表示用户 u 对商品 v的偏好

信任度：变量 ，它衡量了我们观察到的信任度

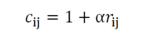
最小化损失函数：

6.  求解：最优化

1）显示和隐式的异同：

• 显示模型只基于观察到的值；隐式需要考虑不同的信任度，最优化时需要考虑所有可能的u，v对

2) 交替最小二乘求解：

即固定 uⁱ 求 vⁱ⁺¹ 再固定 vⁱ⁺¹  求 uⁱ⁺¹

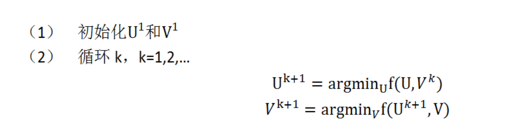
7. 例子

1 2 3 4 5 6 7 8 9 10

import org.apache.spark.mllib.recommendation._<br>//处理训练数据 val data = sc.textFile("data/mllib/als/test.data") val ratings = data.map(_.split(',') match { case Array(user, item, rate) =>   Rating(user.toInt, item.toInt, rate.toDouble) })   // 使用ALS训练推荐模型 val rank = 10 val numIterations = 10 val model = ALS.train(ratings, rank, numIterations, 0.01)

• ALS算法实现于org.apache.spark.ml.recommendation.ALS.scala文件中
• Rating也在recommendation里面

ALS是alternating least squares的缩写 , 意为交替最小二乘法；而ALS-WR是alternating-least-squares with weighted-λ -regularization的缩写，意为加权正则化交替最小二乘法。该方法常用于基于矩阵分解的推荐系统中。例如：将用户(user)对商品(item)的评分矩阵分解为两个矩阵：一个是用户对商品隐含特征的偏好矩阵，另一个是商品所包含的隐含特征的矩阵。在这个矩阵分解的过程中，评分缺失项得到了填充，也就是说我们可以基于这个填充的评分来给用户最商品推荐了。

　　由于评分数据中有大量的缺失项，传统的矩阵分解SVD（奇异值分解）不方便处理这个问题，而ALS能够很好的解决这个问题。对于R(m×n)的矩阵，ALS旨在找到两个低维矩阵X(m×k)和矩阵Y(n×k)，来近似逼近R(m×n)，即：

　　其中R(m×n)代表用户对商品的评分矩阵，X(m×k)代表用户对隐含特征的偏好矩阵，Y(n×k)表示商品所包含隐含特征的矩阵，T表示矩阵Y的转置。实际中，一般取k<<min(m, n), 也就是相当于降维了。这里的低维矩阵，有的地方也叫低秩矩阵。

　　为了找到使低秩矩阵X和Y尽可能地逼近R，需要最小化下面的平方误差损失函数：

　　其中x_u(1×k)表示示用户u的偏好的隐含特征向量，y_i(1×k)表示商品i包含的隐含特征向量, r_ui表示用户u对商品i的评分, 向量x^u和y_i的内积x_u^Ty_i是用户u对商品i评分的近似。

损失函数一般需要加入正则化项来避免过拟合等问题，我们使用L2正则化，所以上面的公式改造为：

　　其中λ是正则化项的系数。

　　到这里，协同过滤就成功转化成了一个优化问题。由于变量xu和yi耦合到一起，这个问题并不好求解，所以我们引入了ALS，也就是说我们可以先固定Y（例如随机初始化X），然后利用公式（2）先求解X，然后固定X，再求解Y，如此交替往复直至收敛，即所谓的交替最小二乘法求解法。

　　具体求解方法说明如下：

• 先固定Y,  将损失函数L(X,Y)对x_u求偏导，并令导数=0，得到：

• 同理固定X，可得：

　　其中ru(1×n)是R的第u行,ri(1×m)是R的第i列， I是k×k的单位矩阵。

• 迭代步骤：首先随机初始化Y，利用公式(3)更新得到X,  然后利用公式(4)更新Y,  直到均方根误差变RMSE化很小或者到达最大迭代次数。

　　上文提到的模型适用于解决有明确评分矩阵的应用场景，然而很多情况下，用户没有明确反馈对商品的偏好，也就是没有直接打分，我们只能通过用户的某些行为来推断他对商品的偏好。比如，在电视节目推荐的问题中，对电视节目收看的次数或者时长，这时我们可以推测次数越多，看得时间越长，用户的偏好程度越高，但是对于没有收看的节目，可能是由于用户不知道有该节目，或者没有途径获取该节目，我们不能确定的推测用户不喜欢该节目。ALS-WR通过置信度权重来解决这些问题：对于更确信用户偏好的项赋以较大的权重，对于没有反馈的项，赋以较小的权重。ALS-WR模型的形式化说明如下：

• ALS-WR的目标函数：

　　其中α是置信度系数。

• 求解方式还是最小二乘法：

　　其中C^u是n×n的对角矩阵，Ci是m×m的对角矩阵；C^u_ii  = c_ui,  Cⁱ_ii  = c_ii。