python(leetcode)-48旋转图像

给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。

说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:
给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],
原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

　这道题其实不难懂，有线性代数基础的人都知道转置矩阵，虽然这题与转置不同但是题目意思相似。90度顺时针旋转矩阵。并且要求不能新建矩阵存储即在原矩阵上操作。

虽然题目不难懂，但是做起来非常麻烦，笔者想了很久才做出这题，主要是逻辑上的思路一定要清晰。

先上代码（通过-44ms)击败99%

class Solution:
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        lens=len(matrix[0])
        for i in range(lens//2):                   #对第i行进行换位操作
            for j in range(i,lens-1-i):            #对第j列进行换位操作
                temp=matrix[i][j]                                       #temp=a
                matrix[i][j]=matrix[lens-1-j][i]                        #a=b
                matrix[lens - 1 - j][i]=matrix[lens-1-i][lens-1-j]      #b=c
                matrix[lens - 1 - i][lens - 1 - j]=matrix[j][lens-1-i]  #c=temp
                matrix[j][lens - 1 - i]=temp

if __name__=="__main__":
    s=Solution()
    matrix = [[1,2],
               [3,4]]
    print(s.rotate(matrix))

上一个简单的思维导图

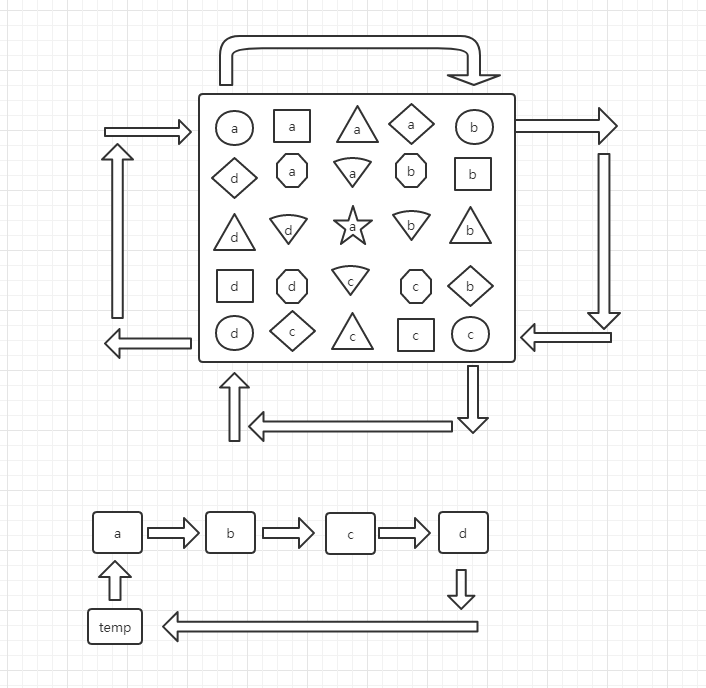
就是做一个旋转的操作 这里的难点有2个地方。

1.a-->b-->c-->d-->temp的对应的下标不能错

2.两层循环中，第二层循环是从i开始到lens-1-i(倒数第i+1个)

然后遇到错误debug看看是否和自己的逻辑一样运行，中途debug了好多次 才理顺 - -！

再看一个评论区大佬的代码（通过44ms)击败99%

class Solution:
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        matrix[:] = zip(*matrix[::-1])

if __name__=="__main__":
    s=Solution()
    matrix = [[1,2],
               [3,4]]
    print(s.rotate(matrix))

真的nb，完美诠释了python的魅力，一行代码解决问题

解释一下

首先解释matrix[::-1] 在list中存在3个参数[a,b,c], a为起始 b为终点 c为步长 

当c<0时 代表倒序，从后往前。并且a和b缺省时，则 [::-1]=[-1,-len()-1,-1] 等于倒叙排列一遍

然后解释zip()函数  zip意为解压  类似于纵向合并  举个例子就明白了

a=[1,2,3]
b=[4,5,6]
ziped =zip(a,b)  #[(1, 4), (2, 5), (3, 6)]
c=[[1,2,3],[4,5,6]]
ziped2=zip(c)    #[(1, 4), (2, 5), (3, 6)]

经过这两部操作，确实可以实现90度旋转

[[1,2,3],  
 [4,5,6],
 [7,8,9]]           

[[7,8,9]
 [4,5,6],
 [1,2,3]]        #[::-1]操作

[[7,4,1],
 [8,5,2],
 [9,6,3]]        # zip()操作