这两周,一直在做搜索类的题目,主要还是集中在深搜和广搜,下周将学习双广和A*。
提到搜索,自然想到图,图这种数据结构,最开始学习的时候特别难。老师常说,树是特殊的图,图也比树一般化很多。深搜和广搜最开始的时候,总是搞不清楚,后来做课设的时候,总算会模拟了。现在才算系统的学习,可以运用自如。也因此,看了一下《算法导论》的搜索部分内容。
1.广度优先搜索
在给定图G=(V, E)和一个特定的源顶点s的情况下,广度优先搜索可以探索G中的边,从而发现s可到达的所有顶点,并计算s到各个可达顶点的距离,并生成以s为顶点、包含所有s可达顶点的最短路径。很多acm题目正是基于广搜的这样的特点而选择使用广搜而不是深搜。其特点是先发现s可达的所有距离为k的顶点,加入队列后,才可探索s可达的所有距离为k+1的顶点。如杭电acm1253,当探测到距离大于最小时间时,证明已经超时,则此时输出结果并返回。其实,这种题目可理解为距离远点为k的可达位置是否满足要求。广搜的时间复杂度是O(V+E),一般广搜都伴随队列。如下图所示: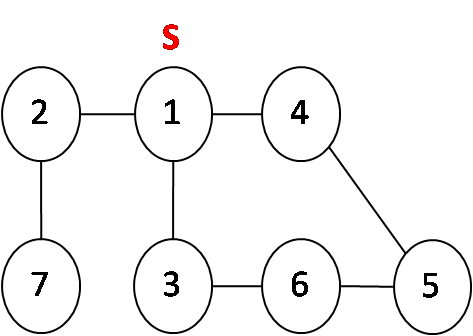
广搜顺序为:1->2->3->4->7->6->5
2.深度优先搜索
相对于广度优先搜索,深度优先搜索更基于更加深的搜索。而且dfs的源点很可能不只一个点,使用这个性质可以区分一部分dfs和bfs,并且当深搜完成后,会回溯会初始点。深搜的写法,也一般采用递归。书中提到,在深搜的同时可以给每个顶点加时间戳,每个顶点v可以有两个时间戳:第一次被发现时的时间戳(d[u]表示)和结束检查v的邻接表时的时间戳(f[u]表示)。使用者两个时间戳的特性也可以解决很多问题。如上图所示的深搜时间戳示意图为:
其实这幅图不太能看出dfs和宽搜的区别,dfs会生成由若干搜索树组成的森林,而不再是一棵树。
3.深度优先搜索的性质
3.1 括号定理
dfs的发现和完成时间具有括号结构(parenthesis structure)。如果把发现顶点u用左括号"("表示,完成用右括号")"表示,那么在各级括号正确嵌套的前提下,发现与完成时间的记载就是一个完整的表达式。如下图所示:
定理22.7 括号定理
在对一个(有向或无向)图G=(V, E)的任何深度优先搜索中,对于图中任意两个顶点u和v,下述三个条件中仅有一个成立:
(1)区间[d[u], f[u]]和区间[d[v], f[v]]是完全不相交的,且在深度优先森林中,u或v都不是对方的后裔;
(2)区间[d[u], f[u]]完全包含于[d[v], f[v]]中,且在深度优先树(注意,此处不是森林)中,u是v的后裔;
(2)区间[d[v], f[v]]完全包含于[d[u], f[u]]中,且在深度优先树(注意,此处不是森林)中,v是u的后裔;
推论22.8(后裔区的嵌套)
在一个(有向或无向)图G中的深度优先森林中,顶点v是顶点u的后裔,当且仅当d[u]<d[v]<f[v]<f[u]。
定理22.9(白色路径定理)
在一个(有向或无向)图G=(V, E)的深度优先森林中,顶点v是顶点u的后裔,当且仅当在搜索过程中于时刻d[u]发现u时,可以从顶点u出发,经过一条完全由白色顶点组成的路径到达v。
边的分类
(1)树边(tree edge)是深度优先森林G‘中的边。如果顶点v是在探寻边(u,v)时被首次发现的,那么(u,v)就是一条树边;
(2)反向边(back edge)是深度优先树中,连接顶点u到它的某一祖先顶点v的那些边。有向图中可能出现的自环也被认为 是反向边;
(3)正向边(forward edge)是指深度优先树中,连接顶点u到它的某个后裔的非树边(u,v);
(4)交叉变(cross edge)是其他类型的边,存在于同一棵深度优先树的两个顶点之间,条件是其中一个顶点不是另一个顶点的祖先。交叉边也可以在不同的深度优先树的顶点之间。
定理22.10
在对一个无向图G进行深度优先搜索的过程中,G的每条边要么是树边,要么是反向边。