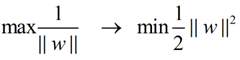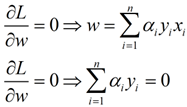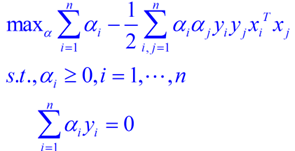线性分类器：
首先给出一个非常非常简单的分类问题（线性可分），我们要用一条直线，将下图中黑色的点和白色的点分开，很显然，图上的这条直线就是我们要求的直线之一（可以有无数条这样的直线）
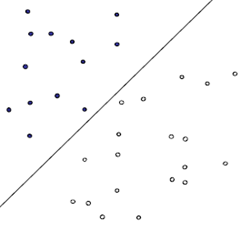假如说，我们令黑色的点 = -1， 白色的点 = +1，直线f(x) = w.x + b，这儿的x、w是向量，其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候，f(x) 表示二维空间中的一条直线， 当x的维度=3的时候，f(x) 表示3维空间中的一个平面，当x的维度=n > 3的时候，表示n维空间中的n-1维超平面。这些都是比较基础的内容，如果不太清楚，可能需要复习一下微积分、线性代数的内容。
刚刚说了，我们令黑色白色两类的点分别为+1, -1，所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。
但是，我们怎样才能取得一个最优的划分直线f(x)呢？下图的直线表示几条可能的f(x)
一个很直观的感受是，让这条直线到给定样本中最近的点最远，这句话读起来比较拗口，下面给出几个图，来说明一下：
第一种分法：
第二种分法：
这两种分法哪种更好呢？从直观上来说，就是分割的间隙越大越好，把两个类别的点分得越开越好。就像我们平时判断一个人是男还是女，就是很难出现分错的情况，这就是男、女两个类别之间的间隙非常的大导致的，让我们可以更准确的进行分类。在SVM中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是由很多道理的，比如说从概率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好，等等。这里就不展开讲，作为一个结论就ok了，:)
上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。
上图就是一个对之前说的类别中的间隙的一个描述。Classifier Boundary就是f(x)，红色和蓝色的线（plus plane与minus plane）就是support vector所在的面，红色、蓝色线之间的间隙就是我们要最大化的分类间的间隙。
这里直接给出M的式子：（从高中的解析几何就可以很容易的得到了，也可以参考后面Moore的ppt）
另外支持向量位于wx + b = 1与wx + b = -1的直线上，我们在前面乘上一个该点所属的类别y（还记得吗?y不是+1就是-1），就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单的将支持向量表示出来了。
当支持向量确定下来的时候，分割函数就确定下来了，两个问题是等价的。得到支持向量，还有一个作用是，让支持向量后方那些点就不用参与计算了。这点在后面将会更详细的讲讲。
在这个小节的最后，给出我们要优化求解的表达式：
||w||的意思是w的二范数，跟上面的M表达式的分母是一个意思，之前得到，M = 2 / ||w||，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，和前面的系数，熟悉的同学应该很容易就看出来了，这个式子是为了方便求导。
这个式子有还有一些限制条件，完整的写下来，应该是这样的：（原问题）
s.t的意思是subject to，也就是在后面这个限制条件下的意思，这个词在svm的论文里面非常容易见到。这个其实是一个带约束的二次规划(quadratic programming, QP)问题，是一个凸问题，凸问题就是指的不会有局部最优解，可以想象一个漏斗，不管我们开始的时候将一个小球放在漏斗的什么位置，这个小球最终一定可以掉出漏斗，也就是得到全局最优解。s.t.后面的限制条件可以看做是一个凸多面体，我们要做的就是在这个凸多面体中找到最优解。这些问题这里不展开，因为展开的话，一本书也写不完。如果有疑问请看看wikipedia。
二、转化为对偶问题，并优化求解:
这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：
求解这个式子的过程需要拉格朗日对偶性的相关知识（另外pluskid也有一篇文章专门讲这个问题），并且有一定的公式推导，如果不感兴趣，可以直接跳到后面用蓝色公式表示的结论，该部分推导主要参考自plukids的文章。
首先让L关于w，b最小化，分别令L关于w，b的偏导数为0，得到关于原问题的一个表达式
将两式带回L(w,b,a)得到对偶问题的表达式
新问题加上其限制条件是（对偶问题）:
这个就是我们需要最终优化的式子。至此，得到了线性可分问题的优化式子。
求解这个式子，有很多的方法，比如SMO等等。
摘自：http://www.cnblogs.com/LeftNotEasy/archive/2011/05/02/basic-of-svm.html