传球问题
问题描述
A,B,C,D,E 五个人互相传球,由 A 开始第一次传球,经 5 次传球后传回到 A 的手上,其中 A 与 B 不会相互传球,C 只会传给 D,E 不会传给 C,共有多少种传法?
分析问题
按照问题的描述可以画出如下的有向图:

传球的模式可以简化为:
A -> □ -> □ -> □ -> □ -> A
实际上可以把它看成一个路径问题,从 A 出发,最终又回到 A。
根据限定条件,尝试不同的路径,经过 5 次传球后,如果能够到达 A,就说明这次尝试的路径是正确的。
可以尝试递归加上回溯解决这个问题。(似乎和找迷宫出路是一样的)
编写代码
使用 ECMAScript 6 编写, node v8.9.4 编译运行。
首先设计一个 Person 类,用来构造 A,B,C,D,E 五个对象。他们内部有一个数组 ableToNext,用来存放可以传球的对象。
class Person {
constructor(name) {
this.name = name;
this.ableToNext = new Array();
}
}
此外有个 persons 对象,存放 5 个人和当前拥有球的人。然后根据当前拥有球的人中存有的 ableToNext 数据,将球传给下一个人,递归地找出所有的可能情况。用一个数组 ballStack 作为栈,用来保存传球的情况。因此栈的大小就是传球的次数。
递归函数 passBall 为:
function passBall(person) {
person.ableToNext.forEach( next => {
// /*
if( ballStack.length < (MaxBallPassCount - 1) && next == persons.finalOwner ) {
// finalOwner doesn't get the ball at the meantime
return;
}
// */
attmptCount++;
ballStack.push( next.name );
persons.ballOwner = next;
// log( ballStack.length +": "+ next+ " " );
passBall(next);
});
// all possiblility have been attempted, get back to last one
ballStack.pop();
}
递归终止的条件是传球 5 次。如果传球的次数达到了 5 次,那么当前拥有球的人就不必继续传球了。
// end condition of recursive
if( ballStack.length == MaxBallPassCount ) {
if( persons.ballOwner == persons.finalOwner ) {
validCount++;
console.log( validCount, ballStack );
}
ballStack.pop();
return;
}
在这里会把所有有效的情况打印出来。不过对于这个问题,由于在 5 次传球的过程中,A 是可以在中间出现的,所以递归函数应该是这样的:
function passBall(person) {
...
person.ableToNext.forEach( next => {
attmptCount++;
ballStack.push( next.name );
persons.ballOwner = next;
// log( ballStack.length +": "+ next+ " " );
passBall(next);
});
...
}
这样得到的有效情况是 30 种:
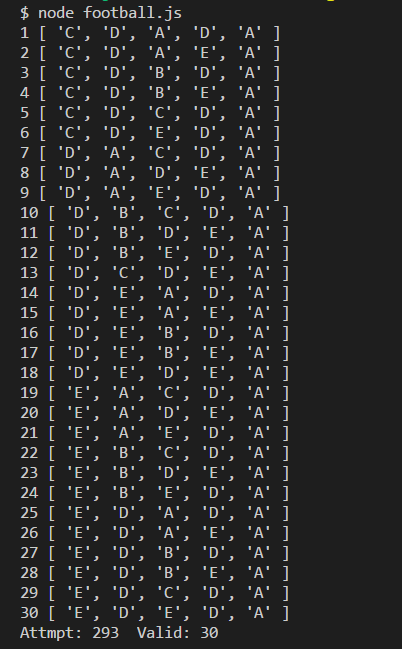
如果说在前 4 次传球过程中,球不能传到 A,那么有效情况是 18 种:
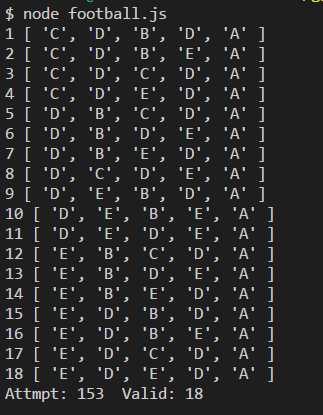
总结
这个问题比较简单,核心内容就是递归函数,最后只要根据限定的次数结束递归就可以得到所有的情况了。
还有 一种思路 是找出所有可能的情况,再根据限制条件进行过滤。
详细的代码在 Github