注：这篇文章源于：https://mp.csdn.net/postedit/99710904， 无需怀疑抄袭，同一个作者，这是我在博客园的账号。
在二叉树中，有两种非常重要的条件，分别是两类数据结构的基础性质。 其一是“堆性质”，二叉堆以及高级数据结构中的所有可合并堆都满足“堆 性质”。 其二是 “BST性质”，它是二叉查找树（Binary Search Tree）以及所有平衡树的基础。
二叉查找树的定义
给定一棵二叉树，树上的每个节点都带有一个数值，成为节点的 “关键码” 。所谓BST性质是指，对于树中的任意一个节点：
·该节点的关键码不小于它的左子树（如果非空）中任意节点的关键码
·该节点的关键码不大于它的右子树（如果非空）中任意节点的关键码 满足上述性质的二叉树就是一棵“二叉查找树”（BST）。 二叉查找树的中序遍历是一个关键码单调递增的节点序列。
二叉查找树的存储
用数组模拟二叉树
1 struct node { 2 int l, r;//左右子节点在数组中的下标 3 int val;//节点关键码 4 }tree[Size];//数组模拟链表 5 int tot;//使用过和正在使用的节点总数量 6 int root;//当前根节点编号，即数组下标
优点：编程复杂度低。不需要考虑分配内存和回收内存
缺点：内存利用率低
用指针表示二叉树
1 struct node { 2 node *l, *r; //指向左右儿子 3 int val;//节点关键码 4 }root;
优点：内存利用率高
缺点：编程复杂度高
二叉查找树的操作
BST支持的操作：
• 树的建立
• 插入关键码为x的节点
• 查询关键码为x的节点的排名
• 求关键码为x的节点的前驱
• 求关键码为x的节点的后继
• 删除关键码为x的节点
二叉查找树的建立
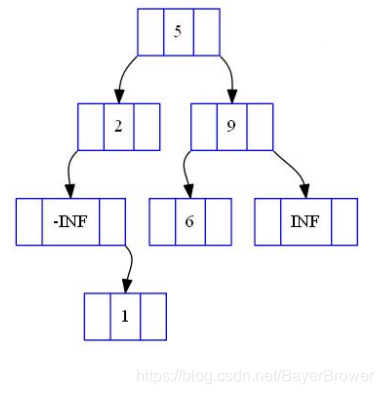
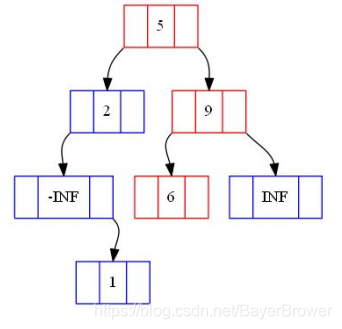
为了避免越界，减少边界情况的特殊判断，编程实现时一般在 BST中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。 仅由这两个节点构成的BST就是一棵初始的空BST。
int New(int val) { a[++tot].val = val; return tot; } void Build() { New(-INF), New(INF); root = 1, a[1].r = 2; }
二叉查找树的检索
在BST中检索是否存在关键码为val的节点。 设变量p等于根节点root，执行以下过程：
1.若p的关键码等于val，则已经找到
2.若p的关键码大于val
a.若p的左子节点为空，则说明不存在val
b.若p的左子节点不空，在p的左子树中递归进行检索
3.若瀃的关键码小于val
a.若p的右子节点为空，则说明不存在val
b.若p的右子节点不空，在p的右子树中递归进行检索
在如下BST中：
查找6：
查找3：
1 int Get(int p, int val) { 2 if (p == 0) return 0; //检索失败 3 if (val == a[p].val) return p; //检索成功 4 if (val < a[p].val) return Get(a[p].l, val); //递归检索左子树 5 else return Get(a[p].r, val);//递归检索右子树 6 }
二叉查找树的插入
在BST中插入一个新的值val（假设目前BST中不存在关键码为val的节点， 若存在则不插入），与BST的检索过程类似。
在发现要走向的p的子节点为空，说明val不存在时，直接建立关键码为 val的新节点作为p的子节点。
1 void Insert(int &p, int val) { 2 if (p == 0) { 3 p = new(val); //p是引用，其父节点的l或r值会被同时更新 4 return; 5 } 6 if (val == a[p].val) return; 7 if (val < a[p].val) Insert(a[p].l, val); 8 else Insert(a[p].r, val); 9 }
二叉查找树找后继
在BST中， val 的后继指的是在关键码大于 val 的前提下，关键码最小的节点。
初始化val为具有正无穷关键码的那个节点的编号(编号为2)。然后，从根节点开始在BST中检索val。在检索的过程中，每经过一个节点，都检查该节点的关键码，判断能否更新所求的后继val。
检索完成后，有三种可能的结果：
1.没有找到val此时val的后继就在已经经过的节点中，val即为所求。
2.找到了关键码为val的节点p，但p没有右子树与上一种情况相同，val即为所求
3.找到了关键码为val的节点p，且p有右子树从p的右子节点出发，一直向左走，就找到了val的后继
1 int GetNext(int val) { 2 int ans = 2; 3 int p = root; 4 while (p) { 5 if (val == a[p].val) { 6 if (a[p].r > 0) { 7 p = a[p].r; 8 while (a[p].l > 0) p = a[p].l; 9 ans = p; 10 } 11 break; 12 } 13 if (a[p].val > val && a[p].val < a[ans].val) ans = p; 14 p = val < a[p].val ? a[p].l : a[p].r; 15 } 16 return a[ans].val; 17 }
二叉查找树找前驱
1 int GetPre(int val) { 2 int ans = 1; 3 int p = root; 4 while (p) { 5 if (val == a[p].val) { 6 if (a[p].l > 0) { 7 p = a[p].l; 8 while (a[p].r > 0) p = a[p].r; 9 ans = p; 10 } 11 break; 12 } 13 if (a[p].val < val && a[p].val > a[ans].val) ans = p; 14 p = val < a[p].val ? a[p].l : a[p].r; 15 } 16 return a[ans].val; 17 }
二叉查找树的删除
从BST中删除关键码为val的节点 首先，在BST中检索val，得到节点p 若p的子节点个数小于2，则直接删除p，并令p的子节点代替p的位置，与p 的父节点相连。 若p既有左子树又有右子树，则在BST中求出val的后继节点next。因为next 没有左子树，所以可以直接删除nest，并令next的右子树代替nest的位置。最后， 再让next节点代替p节点，删除p即可。
1 void Remove(int val) { 2 //检索val， 得到节点p 3 int &p = root; 4 while (p) { 5 if(val == a[p].val) break; 6 p = val < a[p].val ? a[p].l : a[p].r; 7 } 8 if (p == 0) return;//结点不存在 9 if (a[p].l == 0) //没有左子树 10 p = a[p].r; //右子树代替p的位置，p是引用 11 else if (a[p].r == 0) //没有右子树 12 p = a[p].l; //左子树代替p的位置，p是引用 13 else { //求后继 14 int next = a[p].r; 15 while (a[next].l > 0) next = a[next].l; 16 Remove(a[next].val); //next一定没有左子树，直接删除 17 a[next].l = a[p].l, a[next].r = a[p].r; //节点next代替p的位置 18 p = next; 19 } 20 }
二叉查找树的性能分析
在随机数据中，BST一次操作的期望复杂度是O(log n)。然而， BST很容易退化，例如在BST中依此插入一个有序序列，将会得到一条 链，平均每次操作的复杂度都为O(n)。 这样的左右子树大小相差很大的BST是不平衡的。有很多种方法可 以维持BST的平衡，从而产生了各种平衡树。
THE END