记录内容来自《Tensorflow实战Google一书》及MOOC人工智能实践 http://www.icourse163.org/learn/PKU-1002536002?tid=1002700003
--梯度下降算法主要用于优化单个参数的取值, 反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法。
从而神经网络模型在训练数据的孙师函数尽可能小。
--反向传播算法是训练神经网络的核心算法, 它可以跟据定义好的损失函数优化神经网络中参数的取值, 从而使神经网络模型在训练数据集上的损失函数达到一个较小值。
假设损失函数如下:
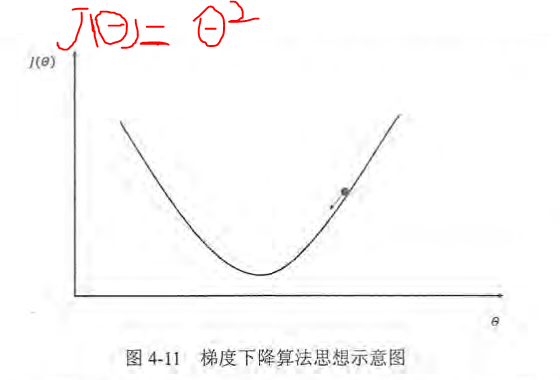
x轴表示参数取值, y轴表示损失函数的值。, 假设当前的参数和损失函数值的位置为图中小黑点的位置, 那么梯度下降算法将会将参数向x轴左侧移动, 从而使小圆点朝箭头的方向
移动。参数的梯度可以通过求骗到的方式计算。

通过以下是实例来解释梯度下降算法作用于损失函数的应用。
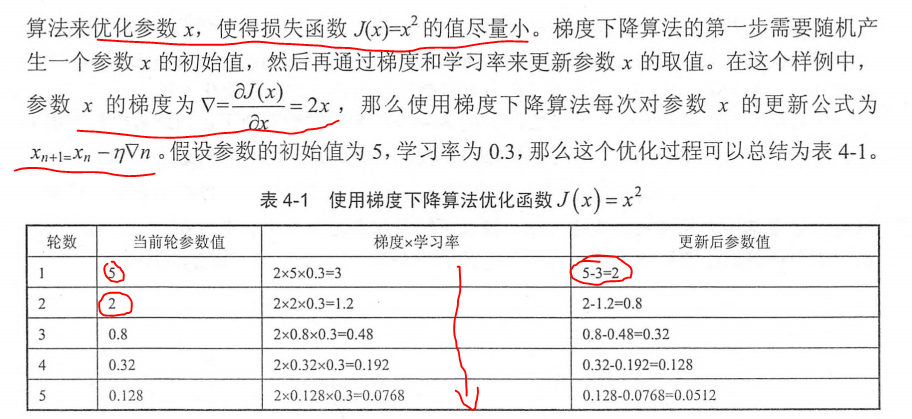
根据例子我们可以看出梯度下降算法可以顺利的使参数值朝着真实的值靠近。但是它并不能保证被优化的函数达到全局最优解。如下图实例所示:

为解决这一问题引进了随机梯度下降算法(stochastic gradient descent):这个算法优化的不是在全部训练数据上的损失函数, 而是在每一轮迭代中,随机优化
某一条训练数据上的损失函数。
神经网络的进一步优化
学习率的设置:
学习率表示了每次参数更新的幅度大小。学习率过大, 会导致待优化的参数在最小值附近波动, 不收敛;学习率过小, 会导致待优化的参数收敛缓慢。
在训练过程中, 参数的更新向着损失函数梯度下降的方向。

一个实例:来自大学MOOCTensorflow笔记
通过梯度下降算法优化损失函数 loss= (w+1)^2, w初始值设置为20, 学习率设置为0.2, 定义反向传播算法最后得到w的值为-1, loss为0, 符合函数曲线。
如果学习率设置为1 则会出现不收敛的情况

1 #coding:utf-8 2 #设损失函数 loss=(w+1)^2, 令w初值是常数5。反向传播就是求最优w,即求最小loss对应的w值 3 import tensorflow as tf 4 #定义待优化参数w初值赋5 5 w = tf.Variable(tf.constant(20, dtype=tf.float32)) 6 #定义损失函数loss 7 loss = tf.square(w+1) 8 #定义反向传播方法 9 train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss) 10 #生成会话,训练40轮 11 with tf.Session() as sess: 12 init_op=tf.global_variables_initializer() 13 sess.run(init_op) 14 for i in range(40): 15 sess.run(train_step) 16 w_val = sess.run(w) 17 loss_val = sess.run(loss) 18 print "After %s steps: w is %f, loss is %f." % (i, w_val,loss_val)
学习率为0.2运行结果如下, 较正常的结果:

学习率为1则会出现震荡不收敛的结果w的值在20和-22之间跳动,这就是不收敛:
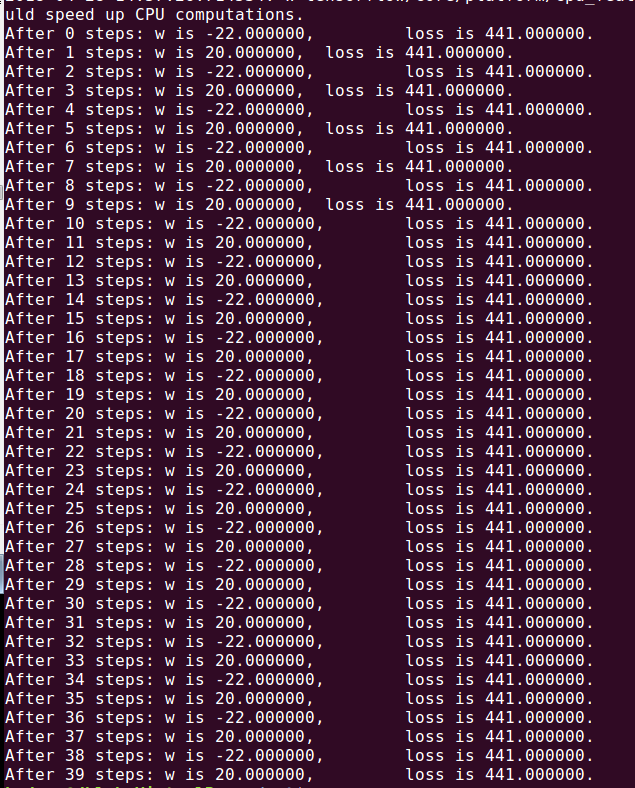
为了解决设定学习率的问题, Tensorflow提供了一种更加灵活的学习率设置方法--指数衰减法
指数衰减学习率: 学习率随着训练轮数变化而动态更新,通过这个函数,可以先使用较大的学习率来快速得到一个比较优的解,然后随着迭代的接续逐步减小学习率,
是的模型在训练后期更加稳定。
学习率计算公式如下:

用 Tensorflow 的函数表示为:
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE,
global_step,
LEARNING_RATE_STEP, LEARNING_RATE_DECAY,
staircase=True/False)
其中, LEARNING_RATE_BASE 为学习率初始值, LEARNING_RATE_DECAY 为学习率衰减率,global_step 记
录了当前训练轮数,为不可训练型参数。学习率 learning_rate 更新频率为输入数据集总样本数除以每
次喂入样本数。若 staircase 设置为 True 时,表示 global_step/learning rate step 取整数,学习
率阶梯型衰减;若 staircase 设置为 false 时,学习率会是一条平滑下降的曲线。

一般来说初始学习率、衰减系数和衰减速度都是根据经验设置的。而且损失函数下降的速度和迭代结束之后总损失的大小没有必然的联系。
也就是说不能通过前几轮损失函数下降的速度来比较不同神经网络的效果。
1 #coding:utf-8 2 #设损失函数 loss=(w+1)^2, 令w初值是常数10。反向传播就是求最优w,即求最小loss对应的w值 3 #使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得更有收敛度。 4 import tensorflow as tf 5 6 LEARNING_RATE_BASE = 0.1 #最初学习率 7 LEARNING_RATE_DECAY = 0.99 #学习率衰减率 8 LEARNING_RATE_STEP = 1 #喂入多少轮BATCH_SIZE后,更新一次学习率,一般设为:总样本数/BATCH_SIZE 9 10 #运行了几轮BATCH_SIZE的计数器,初值给0, 设为不被训练 11 global_step = tf.Variable(0, trainable=False) 12 #定义指数下降学习率 13 learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, LEARNING_RATE_STEP, LEARNING_RATE_DECAY, staircase=True) 14 #定义待优化参数,初值给10 15 w = tf.Variable(tf.constant(10, dtype=tf.float32)) 16 #定义损失函数loss 17 loss = tf.square(w+1) 18 #定义反向传播方法 19 train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step) 20 #生成会话,训练40轮 21 with tf.Session() as sess: 22 init_op=tf.global_variables_initializer() 23 sess.run(init_op) 24 for i in range(40): 25 sess.run(train_step) 26 learning_rate_val = sess.run(learning_rate) 27 global_step_val = sess.run(global_step) 28 w_val = sess.run(w) 29 loss_val = sess.run(loss) 30 print "After %s steps: global_step is %f, w is %f, learning rate is %f, loss is %f" % (i, global_step_val, w_val, learning_rate_val, loss_val)
由结果看出学习率在不断的减小