输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
- 可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
- 你算法的时间复杂度应该为
O(n^2)。
进阶: 你能将算法的时间复杂度降低到 O(N*logN) 吗?
1. 方法一:动态规划
定义状态:dp[i] 表示以第 i 个数字为结尾的最长上升子序列的长度。即在 [0, ..., i] 的范围内,选择 以数字 nums[i] 结尾 可以获得的最长上升子序列的长度。注意:以第 i 个数字为结尾,即 要求 nums[i] 必须被选取。反正一个子序列一定会以一个数字结尾,那我就将状态这么定义,这一点是常见的。
状态转移方程:遍历到索引是 i 的数的时候,我们应该把索引是 [0, ... ,i - 1] 的 dp 都看一遍,如果当前的数 nums[i] 严格大于之前的某个数,那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列。把前面的 i 个数都看了,dp[i] 的值就是它们的最大值加 1 。即比当前数要小的那些里头,找最大的,然后加 1 。
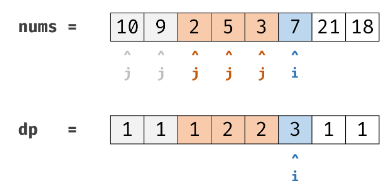
于是状态转移方程是:dp(i) = max{1 + dp(j) if j < i and dp[i] > dp[j]}。
最后不要忘了,扫描一遍这个 dp 数组,其中最大值的就是题目要求的最长上升子序列的长度。
nums = [1,7,9,8,3,4,5]
# dp = [1,2,3,3,2,3,4] # 可以用于输出最长子序列——基于现有评分列表,计算当前item的排名
dp = [1] * len(nums)
for i in range(1, len(nums)):
for j in range(i):
if nums[j] < nums[i]: # 如果要求非严格递增,将此行 '<' 改为 '<=' 即可。
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))
# 输出
[3, 2, 4]
1
2
2. 方法二:贪心算法(二分法)
思路:每一次来一个新的数 num,在 tail 数组(tail 数组的定义在下面的示意图中有)中找大于等于 num 的那个数,试图让它变小,以致于新来的数有更多的可能性接在它后面,成为一个更长的“上升子序列”,这是“贪心算法”的思想。
在 tail 数组中找大于等于 num 的那个数,可以使用“二分法”