树

树状图是一种数据结构。由n(n>=1)个有限节点组成的一个具有层次关系的集合。

满二叉树：

像这种的，所有的叶子节点都是有的。不存在有空的树就是满二叉树。

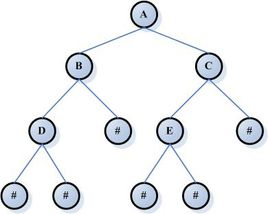
完全二叉树：

这种的也是完全二叉树。只要是连贯的。没有断开的树都是完全二叉树。如果没有3的话。那他就不是完全二叉树了。

我们来看下代码：  链式结构的二叉树

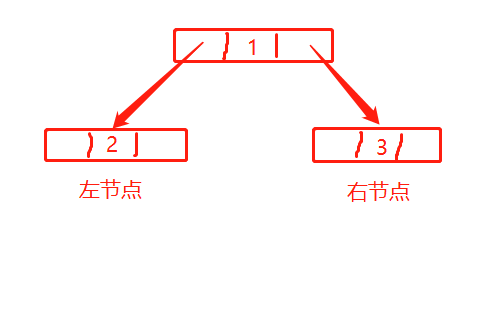
先定义一个树。然后有一个根节点 root

/**
 * 创建一个树。是链式的
 */
public class Tree {
    TreeNode root;

    public TreeNode getRoot() {
        return root;
    }

    public void setRoot(TreeNode root) {
        this.root = root;
    }
}

 然后定义树。因为是链式结构的。每一个节点都可能有左儿子和右儿子。所以定义一个左节点：leftNode  右节点：rightNode;

/**
 * 创建一个树。这个树是链式结构的。
 */
public class TreeNode {
    //树中链式结构的值。
    int value;
    //左儿子
    TreeNode leftNode;
    //右儿子
    TreeNode rightNode;

    public TreeNode(int value) {
        this.value = value;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public TreeNode getLeftNode() {
        return leftNode;
    }

    public void setLeftNode(TreeNode leftNode) {
        this.leftNode = leftNode;
    }

    public TreeNode getRightNode() {
        return rightNode;
    }

    public void setRightNode(TreeNode rightNode) {
        this.rightNode = rightNode;
    }
}

现在测试一下：

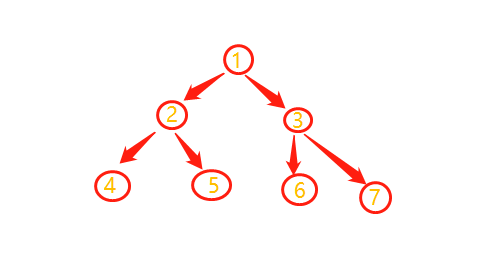
public class TestTree {
    public static void main(String[] args) {
        //创建一个树。
        Tree tree = new Tree();
        //创建根节点
        TreeNode treeNode = new TreeNode(1);
        tree.setRoot(treeNode);
        //创建左儿子
        TreeNode LtreeNode = new TreeNode(2);
        treeNode.setLeftNode(LtreeNode);
        //左儿子再创建第三代的左儿子和右儿子
            //创建左儿子的左儿子
            TreeNode LLtreeNode = new TreeNode(4);
            LtreeNode.setLeftNode(LLtreeNode);
            //创建左儿子的右儿子
            TreeNode RRtreeNode = new TreeNode(5);
            LtreeNode.setRightNode(RRtreeNode);
        //创建右儿子
        TreeNode RtreeNode = new TreeNode(3);
        treeNode.setRightNode(RtreeNode);

        //创建右儿子的左儿子
        TreeNode RLtreeNode = new TreeNode(6);
        RtreeNode.setLeftNode(RLtreeNode);
        //创建右儿子的右儿子
        TreeNode RRRtreeNode = new TreeNode(7);
        RtreeNode.setRightNode(RRRtreeNode);
         }
}

这样就创建了一个这样的树。

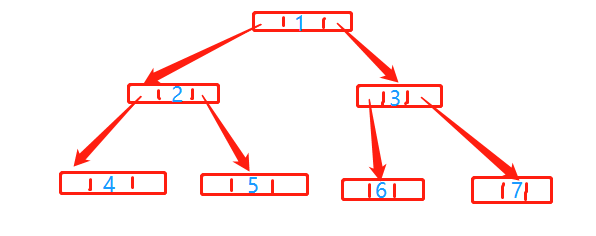
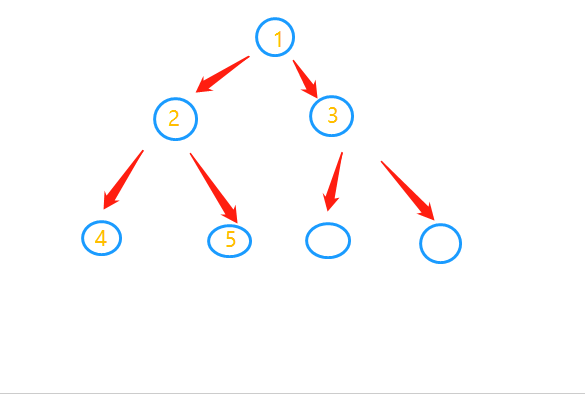
现在树已经创建好了。我们来遍历一下。

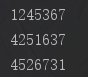
前序遍历。就是先找自己，就是根，然后左节点，右节点。  先找1  ，然后该是2和3了。但是2和4  5又是一个小树（这里 用到了递归。自己调用自己。）。所以就去找4，5  然后是3  6  7  这个顺序是：1 2 4 5 3 6 7 .

中序遍历。把自己放到中间去找。先找左节点。然后就是自己。再就是右节点。 顺序是：4 2 5 1  6 3 7

后序遍历：把自己放到最后查找。现在左节点。右节点。自己  。顺序：4  5  2  6  7  3  1 

我们看下代码：在TreeNode 类种。

 //前遍历
    public void frontShow(){
        //自己放在第一个进行遍历
        System.out.print(value);
        //左节点
        if(leftNode!=null){
            leftNode.frontShow();
        }
        //右节点
        if (rightNode != null) {
            rightNode.frontShow();
        }
    }

    //中遍历
    public void midShow(){
        //左节点
        if(leftNode!=null){
            leftNode.midShow();
        }
        //自己放在中间进行遍历
        System.out.print(value);
        //右节点
        if (rightNode != null) {
            rightNode.midShow();
        }
    }

    //后遍历
    public void afterShow(){
        //左节点
        if(leftNode!=null){
            leftNode.afterShow();
        }
        //右节点
        if (rightNode != null) {
            rightNode.afterShow();
        }
        //自己放在最后进行遍历
        System.out.print(value);
    }

测试：

 //前序遍历
        treeNode.frontShow();
        System.out.println();
        //中序遍历
        treeNode.midShow();
        System.out.println();
        //后序遍历
        treeNode.afterShow();
        System.out.println();

结果：

我们看下查找一个节点：

 //前序查找
    public TreeNode frontSearch(int i) {
        TreeNode treeNode = null;
        //先和自己进行比较。如果值相同的话，就直接返回就行了。
        if(this.value == i){
            return this;
        }
        //左儿子。和左节点进行比较。如果有左节点。然后去查找。
        if(leftNode != null){
            treeNode = leftNode.frontSearch(i);
        }
        //返回的值不为null，就是找到了。
        if(treeNode!=null){
            return treeNode;
        }
        //右儿子。左边的没有找到。找右边的。
        if(rightNode!=null){
            treeNode = rightNode.frontSearch(i);
        }
        return treeNode;
    }

我们看删除一个节点：

在链表类中的方法实现。

//删除。
    public void delete(int i){
        //先判断要删除的是不是自己。
        TreeNode deleteTreeNode = this;
        //左叶子。
        if(deleteTreeNode.leftNode!=null && deleteTreeNode.leftNode.value==i){
            deleteTreeNode.leftNode = null;
            return;
        }
        //右叶子。
        if(deleteTreeNode.rightNode!=null && deleteTreeNode.rightNode.value==i){
            deleteTreeNode.rightNode = null;
            return;
        }
        //看看要删除的是不是左叶子的两个左右节点。
        deleteTreeNode = leftNode;
        if(deleteTreeNode != null){
            deleteTreeNode.delete(i);
        }
        deleteTreeNode = rightNode;
        if(deleteTreeNode != null){
            deleteTreeNode.delete(i);
        }
    }

在树中的方法实现。

 //删除
    public void delete(int i) {
        if(root.value == i){
            root = null;
        }else {
            root.delete(i);
        }
    }

测试：

//删除
        tree.delete(2);
        tree.frontShow();

显示前序遍历：

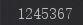
删除的是2：

删除5：

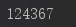
删除1：