马上要迎来2018年了。
新的一年希望自己可以系统的学习一下机器学习的基础，先从统计基础开始吧。
加和值
我们生活中几乎处处可以见到应用的实例。
例如：我这次去旅游一共花了2000元；2015年中国人民共和国GDP（国内生产总值）为68.91万亿元；这个班同学的成绩综合是600分。
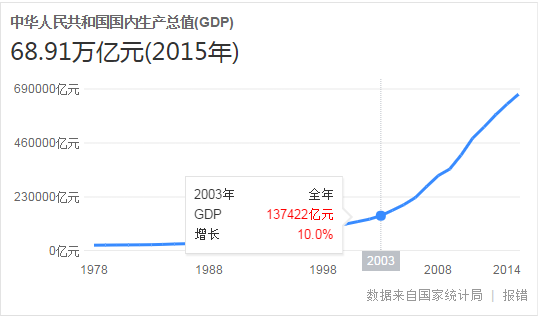这些都是用加和值来描述一个实物。
一般我们把“加和值”的概念用希腊字母 ∑ 表示，读作Sigma
算数平均值
学生时代经常遇到平均值大概都是在描述考试成绩的时候，如果还继续应用我们上面的提到的加和值的话，如果班级和班级之间人数不一样，那这个值就没用参考意义了，例如：一班40人，加和值3440；二班60人，加和值4200分；三班50人，加和值4300；，我们很难从这个数值中看出哪个班的实力强弱。但是如果我们用平均分表示：
一班40人，平均分86分
二班60人，平均分70分
三班50人，平均分86分
我们就可以非常清楚的看出来，一班和三班的水平差不多，高于二班。所有这类用单一的数据定义来概括性描述一些抽象或复杂数据的方式方法叫“指标”。而算数平均值就是我们平时用的一个衡量指标。
算数平均值的计算公式为：
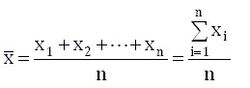
标准差
标准差（Standard Deviation），又常称均方差，是离均差平方的算术平均数的平方根，用σ表示（σ为希腊字母，也读做Sigma）。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。我们还是以学生的成绩来对这个指标进行描述。
这里运用标准差可以表示出哪个班的同学的成绩整体比较稳定，和平均值之间的差距不大。
标准差的计算公式为：
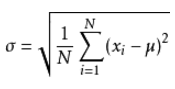
加权平均
带权重（Weight）的平均值，一般我们在特定的场合下。例如下面
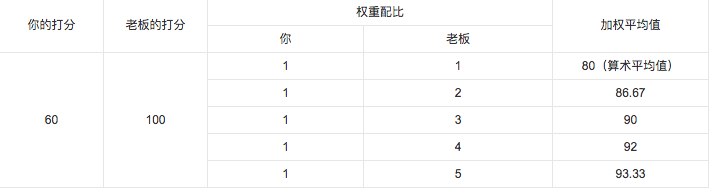
所以总结来说，加权平均值的计算公式为：若n个数 x1,x2, …,xn 的权分别是 w1,w2,…,wn ，那么结果为：
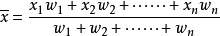
众数
举个简单的例子来理解。一位理发师对今天来理发的客人的年龄进行了一个登记，得到“13，54，33，20，67，21，33” ，其中33出现了两次，是这组数据中出现最多的数字，因此33就是众数。当然最终众数的应用可能不只是数字，有可能是其他的数据类型，例如我今年每个月去看一次电影，其中“警匪片”看了5次，其他都是1词，那么“警匪片”就是“众数”
中位数
顾名思义就是位于中间位置的数字，例如这次来体检的人身高，由大到小排列依次为“165，170，173，178，180，185，191，198” ，那么中位数就是（178+180）/2 = 179。
我们生活中用算数平均值用的比较多，很少用众数和中位数来表示，主要原因在于生活中很多的事物都遵循正态分布（后面介绍），正态分布中平均值、中位数、众数是比较接近的。
欧式距离
也称欧几里得距离（Euclidean distance），用来表示欧几里得空间中两点间“普通”（即直线）距离。
在欧几里得空间中，点x =(x1,...,xn)和 y =(y1,...,yn)之间的欧氏距离为：
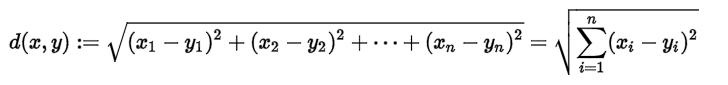
一般情况下，我们计算二维空间比较多，例如（1，3）和（3，2）两个点的距离就为：根号5
曼哈顿距离
曼哈顿距离（Manhattan Distance）也叫出租车距离，解析几何中常用的的一种计算方法，计算比较简单，不需要借助平方和开方。计算公式为：
C = |x1-x2| + |y1-y2|
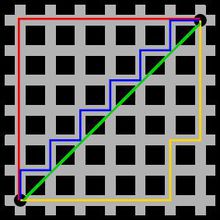
图中三条线的曼哈顿距离都是相等的。
同比、环比
我们直接看例子，2018年2月份的收入，同比增长80%，环比增长6%。
同比代表的意思就是直接和上一次同一时期（2017年的2月份）直接比较，而环比是和上一次的数据（2018年1月份）进行比较。
需要注意的是，当我们要关注同比和环比的时候，对这两个指标的周期我们需要选择一个合适的时间，例如体检可以用年来表示，公司财务可以用季度，网站的访问量就可以用日PV（Page view）。
高斯分布
高斯分布又叫正态分布，是一个在数学、物理、工程领域都非常重要的概率分布，在统计学中应用中也有着很大影响力。
先看看高斯分布的概率密度函数公式：
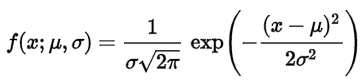
先简单介绍一下概率密度函数。
学生时代我们经常用 y=f(x) 来表示 x 这个自变量和 函数值 y 之间的关系，f(x) 展开后就解释了 x 具体参与运算的一个过程。而概率密度的 y=f(x) 中，x代表样本特征的自变量，y是x在这个样本特征性的数量比例。
exp，代表以e（无理数，约为2.71828）为底的多少次方，即e的多少次幂。y=exp(x) 的函数图像如下：
所以概率密度函数 在 x = μ 的时候，函数到达峰值，即 1/(σ*根号(2π))
这里样本数量的计算用的是定积分的概念，即整个函数曲线与下方x轴围成的面积占比。在 x = μ 的两侧对称。其中x 在x-σ和x+σ之间的样本数量占到整个样本数量的68.2%，在x-2σ和x+2σ之间的样本数量占到整个样本数量的95.4%，在x-3σ和x+3σ之间的样本数量占到整个样本数量的99.6%。
高斯概率密度函数的函数曲线图如下所示：
高斯分布做为分布特征的，主要用来描述统计的对象，如果我们统计的对象符合高斯分布的话，那么高斯分布的的一些经验我们就可以直接的使用。日常生活中符合高斯分布的例子非常的多，用普通的一句话来概括就是“普通的很多，极端的很少”。
举个实际的例子，假如我们某地区男性的身高随机做了些抽样，一共1000个人，最后得到的结论是他们的身高是 以 μ=175cm σ=10cm 的高斯分布。那么这样的描述就可以准确的描述这些样本的分布特征了，对于的我们也可以得到以下这些结论：
175~185 和 165~175 都是 341人；
155~165 和 185~195 都是 136人；
145~155 和 195~205 都是 21人；
这些数量基本上已经涵盖99.6%的人了，当然在不同的情况下，对应的 μ 和 σ 可能都是不一样的。μ 的大小直接影响了整个函数图像在坐标轴上的前后位置，σ 的大小直接影响了函数图像的一个陡峭程度。
泊松分布
一种统计与概率学常见的离散概率分布。泊松分布的概率函数为：
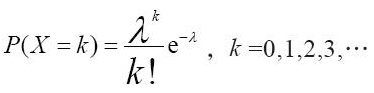
公式中的 λ 是单位时间（或单位面积）随机事件的平均发生率。 泊松分布适合于描述单位时间内随机时间发生的次数。泊松分布概率密度函数：
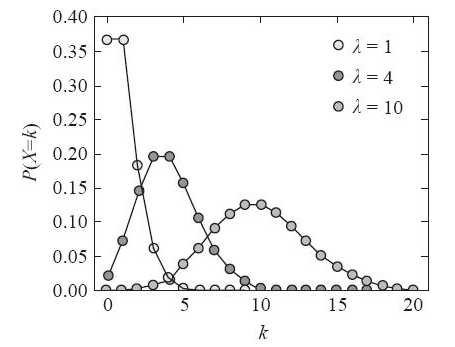
泊松分布说的是在一个标准的时间里，发生这件事的发生率（次数）是 λ ，那么发生 K 次的概率是多少。
泊松分布适用的事件需要满足以下3个条件：
1、这个事件是一个小概率事件；
2、事件每次发生是相对独立的，不相互影响；
3、事件的概率是稳定。
举个泊松分布例子来说明一下：一个公交车站有不同线路的车驶入，平均每5分钟会来两辆车，那么5分钟来5辆车的概率多大。
这里 λ = 2， k = 5，直接带入公式即可。
上面的例子比较简单，我们看一个稍微比较复杂的例子。
已知一个书店，计算机类数销量一直比较稳定，平均每周卖出4本《设计模式》，那么老板应该准备多少本比较合适？
这其实就是典型泊松分布的例子，已知 λ = 4，其实是求 k 为多少合适，这里的合适就看“累计概率” 到达多少后能满足你的要求，我们先计算出每种情况下的概率分布：
P(X=k=1) = 41÷1*e-4=4÷1÷e4 = 7.33%
P(X=k=2) = 42÷(2*1)*e-4 = 14.7%
P(X=k=2) = 43÷(3*2*1)*e-4 = 19.5%
P(X=k=2) = 44÷(4*3*2*1)*e-4 = 19.5%
P(X=k=2) = 45÷(5*4*3*2*1)*e-4 = 15.6%
P(X=k=2) = 46÷(6*5*4*3*2*1)*e-4 = 10.4%
P(X=k=2) = 47÷(7*6*5*4*3*2*1)*e-4 = 5.95%
P(X=k=2) = 48÷(8*7*6*5*4*3*2*1)*e-4 = 2.98%
P(X=k=2) = 49÷(9*8*7*6*5*4*3*2*1)*e-4 = 1.32%
我们列出累计概率：
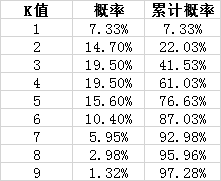
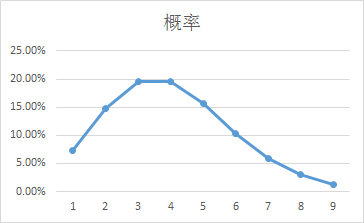
其实我们可以观察，图中的曲线和x轴围成的面积，就是我们要计算的累计概率。我们用最终累计概率来完成这个题目的话就可以这样解释：假如我们进9本的话，大概有97.28%的销售周不会出现供不应求，一年52个周，大概只会有一周脱销。然而我们看到当K值增加到一定数量的时候，K即使在变大，其实概率的增长已经特别小了，所以一般在实际情况中，还会根据成本来决定进书的数量，这里选择5比较合适，还记得高斯分布68.2%的分布就可以代表大多数的情况了，而这里的概率已经超过了68.2%，因此5本在实际中就够用了。
伯努利分布
也叫二项分布，零一分布，也是一种离散分布。分布规律如下：
看上去是个分段函数，其实也可以表示为：
P(n) = pn(1-p)1-n
上式中只需要把n=0和n=1带入，就可以得到上面的分段公式。
伯努利分布必须满足的条件是：
1、各次试验中的事件都是相互独立的，每一次n=1和n=的概率分别为p和q；
2、每次实验都只有两种结果，即n=0或者n=1。
如果不满足上述条件就不是伯努利分布。
如果一次实验满足：P(n) = pn(1-p)1-n 那么连续实验n次的情况下，出现n=1恰好发生k次的概率为：
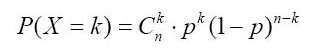
Cnk 即 n!/(k!(n-k)!) 下面用一个例子来说明一下：
小明参加“百万英雄”答题，每次通过的概率为1/3，不通过的概率为2/3，如果他连续参加4天，那么恰好两次通过的概率是多少？
这个问题里，p=1/3, n=4, k=2 ，那么我们直接带入公式 就可以得到：
P(X = 2) = 4*3*2*1/(2*1(2*1)) * (1/3)2*(1-1/3) 4-2 = 8/27
当然这道题目，我们也可以使用排列组合的方式进行计算，最终得到的答案也是这样的。然而有的时候当n和k比较大的时候，那我们就需要用伯努利分布来计算啦。
——学习笔记出自 http://yuedu.163.com/book_reader/9b064430c98d4dd49534092f3d087a66_4