熵

前言

---

　　不要怀疑自己，这个字就是读shang，哈哈。这一节主要说一下“信息熵”。

　　当然在介绍信息熵之前，先需要了解一下信息量以及热力熵。

信息量

---

　　信息，指音讯、消息、通讯系统传输和处理的对象，泛指人类社会传播的一切内容。1948年，数学家香农在题为“通讯的数学理论”的论文中指出：“信息是用来消除随机不定性的东西”。

　　我们在生活中得到的信息，经常也能帮助我们消除一些不定性的东西，例如一场势钧力敌的比赛，在比赛开始前，我们无法预知比赛的结果，然而当我们得到“蓝队的多位主力由于流感病毒而无法上场”这个信息后，就能帮助我们推断，这场比赛很有可能红队会获胜。这里我们就可以认为，这个消息的“消息量较大”，足够我们判断出最终比赛的结果，然而这个信息量究竟是多大呢？能否量化呢，这就是我们下面要介绍的。

　　信息量的想法最早在1928年由R.V.L.Hartley首先提出，他将消息数的对数（log）定义为信息量。如果信源有M种消息，且每个消息是以相等可能产生的，那么该信源的信息量可以表示为：

I = log₂M

　　看一下y=log₂x的函数曲线图

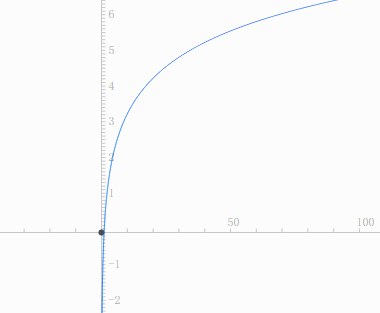
　　只看公式不好理解，我们看一个实际的例子：

　　美国男篮和中国男篮打比赛，结果只有可能是2种（中国胜美国败、美国胜中国败），所以它的信源m=2。根据公式I=Log₂2=1，信息量为1；

　　世界杯淘汰赛有32支进行比赛，突然被告知一个球队获胜的信息量I=log₂32=5（这里的信源是32，因为最终32个球队都有可能获胜）；

　　极端情况，只有一种可能性的情况下，I=log₂1=0，这个代表的含义就是即使被告知了结果，也没用任何价值，即信息量为0。例如博尔特和我比赛跑步，博尔特获胜。

　　看了上面的例子，很多人都会有疑问。美国男篮和中国男篮获胜的信息量都为1，但是我怎么觉得“美国男篮一定会赢呢？”，那么是否可以说美国男篮的信息量为0呢？

　　按照理论上来说，消除的不确定程度越高，信息量就越大；消除的不确定程度越低，信息量越小。

　　其实我们刚才在使用I=log₂M这个公式的时候，有一个隐含的前提，就是m种情况产生的概率是均等的。而我们刚才的例子中其中一种情况（美国男篮）可能性已经非常的高了，并不是等概率事件。因此我们要换一个公式来进行计算信息量了：

H_(x) = -log₂P

　　这里x表示一个发生的事件，P表示这个发生的先验概率。先验概率就是这个事件按照常理发生的概率。

　　继续用美国男篮和中国男篮做例子，假如两队历史上，美国对阵中国20场剩19场（这里只是举例，据我了解美国男篮应该还没输过），那么 19/20 就是美国队获胜的先验概率。我们再计算一下：

　　美国获胜的信息量：H_{(美国获胜)} = -log₂(19/20) = 0.074

　　中国获胜的信息量：H_{(中国获胜)} = -log₂(1/20) = 4.32

　　这下觉得这个值是不是更加合理了。

　　

热力熵

---

　　热力学中的熵最早由德国物理学家克劳修斯于1865年所提出。用一个简单的生活小例子说明一下：

　　在一个U型槽中，放一个小铁球，在没有空气和没有摩擦力的情况下，小球从一端下落最后会上升到另一端，周而复始的做着重复的过程，当然这是理想状态下。

　　在现实生活中，由于空气的阻力和小球与槽之间的摩擦力最终会导致，小球势能转换为动能的时候有一定的损失，最终小球会越来越低，直到停止。在整个的过程中，机械能变成了不可逆的内能，即整个系统的发热，温度增加，最终熵增加。看来熵的增加并不是一件好事，有物理学家扩大了热力熵存在的场景，放到了宇宙中去，提出热寂理论，即宇宙也是由原子之间的斥力和引力所提供的能力在运动，其实类似于“U型槽”，随着熵的增加，最终机械能会慢慢的小号，最终宇宙一片死寂。当然这只是猜测，没有得到证实。

信息熵

---

　　信息熵的出现主要是为了对“信息复杂程度/杂乱程度”的一个量化，它到公式为：

$H(x) = -sumlimits_{i=1}^{n} P(x_{i})log_{2}P(x_{i}) , i=1,2,...,n $

　　其中x代表一个信源，就是该信源到概率乘以该信源到信息量，然后做加和即可。这里需要注意，有些地方到计算可能不是log以2为底，而是以10或者e为底，这里都是可以到，但是需要注意到一点就是，在一次参与运算到其中，需要使用同一个底数来进行计算。

　　举几个例子我们一起看看：

　　1、两两pk，实力悬殊

　　例如美国男篮和中国男篮到比赛，历史上一共交手了64次，其中美国胜63次，中国胜一次。那么可以得到：

　　中国获胜的信息量：-log₂(1/64) = 6 ；  美国获胜的信息量：-log₂(63/64) = 0.023

　　所以美国男篮和中国男篮到比赛到信息熵是 ： 6*(1/64) + 0.023*(63/64) = 0.1164

　　2、两两pk，水平差不多

　　例如费德勒和纳达尔进行一场网球比赛，两个人获胜到胜利都是1/2。那么可以得到：

　　费德勒获胜的信息量：-log₂(1/2) = 1 ；  纳达尔获胜的信息量：-log₂(1/2) = 1

　　所以费德勒和纳达尔进行一场网球比赛到信息熵是 ： 1*(1/2) +1*(1/2) = 1

　　3、32选一，实力悬殊

　　比如32支队伍打比赛，A队获胜到概率为99%，其余31只队获胜到概率为：1%/31。那么可以得到：

　　A队获胜的信息量：-log₂(99%) = 0.0145 ；  其余各个队获胜的信息量：-log₂(0.01/31) = 11.60

　　所以这次比赛到信息熵是 ： 99%* 0.0145 + (0.01/31)*11.60 +..... + (0.01/31)*11.60= 0.130

　　4、32选一，实力差不多

　　比如32支队伍打比赛，各个队伍获胜到概率都是 1/32。那么可以得到：

　　每只队获胜的信息量：-log₂(1/32) = 5；

　　所以这次比赛到信息熵是 ： 1/32 * 5 + 1/32 * 5 +..... + 1/32 * 5 = 5

　　从上述到例子中我们可以得到到结论就是：

　　信息越准确，越单一，信息熵越小；

　　信息越不确定，越混乱，信息熵越大。

　　由于信息熵可以代表信息到混乱程度，所以凡是需要关注到信息混乱程度对信息系统影的地方都可以用信息熵来辅助调整和判断。后面还会有再用到信息熵的地方，到时候我们再回顾。